练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．复数$\frac{2+i}{1-i}$在复平面内对应的点在（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    分析 利用复数代数形式的乘除运算化简，求出复数$\frac{2+i}{1-i}$在复平面内对应的点的坐标得答案．

    解答 解：∵$\frac{2+i}{1-i}$=$\frac{（2+i）（1+i）}{（1-i）（1+i）}=\frac{1+3i}{2}=\frac{1}{2}+\frac{3}{2}i$，
    ∴复数$\frac{2+i}{1-i}$在复平面内对应的点的坐标为（$\frac{1}{2}，\frac{3}{2}$），位于第一象限．
    故选：A．

    点评 本题考查复数代数形式的乘除运算，考查了复数的代数表示法及其几何意义，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    10．设数列{an}的前n项和为Sn，若a1=1，an+1=3Sn（n∈N*），则S6=（　　）
    A．44B．45C．$\frac{1}{3}•$（46-1）D．$\frac{1}{3}•$（45-1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．已知等比数列{an}的公比为q，前n项和为Sn，若点（n，Sn）在函数y=2n+1+m的图象上，则m=-2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知函数f（x）=（a-1）lnx-$\frac{1}{2}$x2，若?x1，x2∈（0，+∞），且x1≠x2，恒有$\frac{f（{x}_{1}）-f（{x}_{2}）}{{x}_{1}-{x}_{2}}$＞0成立，则实数a的取值范围是（　　）
    A．[1，+∞）B．（-∞，-1]C．（-∞，1]D．[-1，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．如图，已知线段AB长度为a（a为定值），在其上任意选取一点M，在AB的同一侧分别以AM、MB为底作正方形AMCD、MBEF，⊙P和⊙Q是这两个正方形的外接圆，它们交于点M、N．试以A为坐标原点，建立适当的平面直角坐标系．
    （1）证明：不论点M如何选取，直线MN都通过一定点S；
    （2）当$|AM|=\frac{1}{3}|AB|$时，过A作⊙Q的割线，交⊙Q于G、H两点，在线段GH上取一点K，使$\frac{1}{|AG|}+\frac{1}{|AH|}$=$\frac{2}{|AK|}$求点K的轨迹．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．命题“?x∈R，x2≠x”的否定是（　　）
    A．?x0∈R，x${\;}_{0}^{2}$=x0B．?x∈R，x2=xC．?x0∉R，x${\;}_{0}^{2}$≠x0D．?x∉R，x2≠x

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．下列命题正确的是（　　）
    A．若p，q为两个命题，则“p且q为真”是“p或q为真”的必要不充分条件
    B．若p为：?x∈R，x2+2x≤0则￢p为：?x∈R，x2+2x＞0
    C．命题p为真命题，命题q为假命题．则命题p∧（￢q），（￢p）∨q都是真命题
    D．命题“若￢p，则q”的逆否命题是“若p，则￢q”．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．已知定圆A：（x+$\sqrt{3}$）2+y2=16动圆M过点B（$\sqrt{3}$，0），且和定圆A相切，动圆的圆心M的轨迹记为C，则曲线C的方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．函数g（x）=2cos（x-$\frac{π}{4}$）cos（x+$\frac{π}{4}$）的图象上各点的横坐标伸长为原来的2倍（纵坐标不变）后得到h（x）的图象，设f（x）=$\frac{1}{4}$x2+h（x），则f′（x）的图象大致为（　　）
    A．B．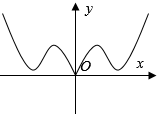
    C．D．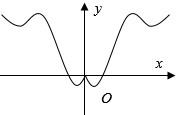

    查看答案和解析>>

    同步练习册答案