
分析 (1)f(x)在(0,a]上是增函数,在[a,+∞)上是减函数,可得f(x)max=f(a)=a2(2lna-1),分类讨论,结合函数的单调性,从而确定函数f(x)在区间(1,e2)上零点的个数;
(2)由h(x)=0,得$lnx-\frac{1}{x}=ax$,结合题意可得$ln{x}_{1}-\frac{1}{{x}_{1}}=a{x}_{1}$,$ln{x}_{2}-\frac{1}{{x}_{2}}=a{x}_{2}$,变形得$\frac{ln\frac{{x}_{2}}{{x}_{1}}}{{x}_{2}-{x}_{1}}+\frac{1}{{x}_{1}{x}_{2}}=a$,转化为$ln{x}_{1}{x}_{2}-\frac{2({x}_{1}+{x}_{2})}{{x}_{1}{x}_{2}}=\frac{{x}_{1}+{x}_{2}}{{x}_{2}-{x}_{1}}•ln\frac{{x}_{2}}{{x}_{1}}$,
不妨令0<x1<x2,记t=$\frac{{x}_{2}}{{x}_{1}}$>1,令F(t)=$lnt-\frac{2(t-1)}{t+1}$(t>1),则F′(t)=$\frac{(t-1)^{2}}{t(t+1)}$>0,由导数确定单调性,可得F(t)=$lnt-\frac{2(t-1)}{t+1}$>F(1)=0,得到$ln\frac{{x}_{2}}{{x}_{1}}$>$\frac{2({x}_{2}-{x}_{1})}{{x}_{1}+{x}_{2}}$,利用不等式放缩可得$ln\sqrt{{x}_{1}{x}_{2}}-\frac{2}{\sqrt{{x}_{1}{x}_{2}}}$>1,再令G(x)=lnx-$\frac{2}{x}$,则x>0时,G′(x)=$\frac{1}{x}+\frac{2}{{x}^{2}}$>0,可得G(x)在(0,+∞)上单调递增,结合ln$\sqrt{2}e$-$\frac{2}{\sqrt{2}e}$=$\frac{1}{2}$ln2+1$-\frac{\sqrt{2}}{e}$≈0.85<1,可得G($\sqrt{{x}_{1}{x}_{2}}$)=$ln\sqrt{{x}_{1}{x}_{2}}$$-\frac{2}{\sqrt{{x}_{1}{x}_{2}}}$>1>$ln\sqrt{2}e-\frac{2}{\sqrt{2}e}$,即$\sqrt{{x}_{1}{x}_{2}}$$>\sqrt{2}e$,得x1•x2>2e2.
解答 (1)解:∵f(x)=2a2lnx-x2,∴f′(x)=$\frac{-2(x-a)(x+a)}{x}$.
∵x>0,a>0,∴当0<x<a时,f′(x)>0,当x>a时,f′(x)<0.
∴f(x)在(0,a]上是增函数,在[a,+∞)上是减函数.
∴f(x)max=f(a)=a2(2lna-1),
讨论函数f(x)的零点情况如下.
①a2(2lna-1)<0,即0<a<$\sqrt{e}$时,函数f(x)无零点,在(1,e2)上也无零点;
②当a2(2lna-1)=0,即a=$\sqrt{e}$时,函数f(x)在(0,+∞)内有唯一零点a,而1<a<e2,
∴f(x)在(1,e2)内有一个零点;
③当a2(2lna-1)>0,即a>$\sqrt{e}$时,
由于f(1)=-1<0,f(a)=a2(2lna-1)>0.f(e2)=(2a-e2)(2a+e2),
当2a-e2<0时,即$\sqrt{e}$<a<$\frac{{e}^{2}}{2}$时,1<$\sqrt{e}$<a<$\frac{{e}^{2}}{2}$<e2,f(e2)<0,
由单调性可知,函数f(x)在(1,a)内有唯一零点x1、在(a,e2)内有唯一零点x2满足,
∴f(x)在(1,e2)内有两个零点;
当2a-e2≥0时,即a≥$\frac{{e}^{2}}{2}$>$\sqrt{e}$时,f(e2)≥0,而且f($\sqrt{e}$)=a2-e>0,f(1)=-1<0,
由单调性可知,无论a≥e2还是a<e2,f(x)在(1,$\sqrt{e}$)内有唯一的一个零点,
在[$\sqrt{e}$,e2)内没有零点,从而f(x)在(1,e2)内只有一个零点;
综上所述,有:当0<a<$\sqrt{e}$时,函数f(x)无零点;
当a=$\sqrt{e}$或a≥$\frac{{e}^{2}}{2}$时,函数f(x)有一个零点;
当$\sqrt{e}$<a<$\frac{{e}^{2}}{2}$时,函数f(x)有两个零点.
(2)证明:h(x)=f(x)-g(x)=2a2lnx-x2+x2-2a3x-$\frac{2{a}^{2}}{x}$=$2{a}^{2}lnx-2{a}^{3}x-\frac{2{a}^{2}}{x}$.
由h(x)=0,得$lnx-\frac{1}{x}=ax$,
由题意知$ln{x}_{1}-\frac{1}{{x}_{1}}=a{x}_{1}$,$ln{x}_{2}-\frac{1}{{x}_{2}}=a{x}_{2}$,
两式相加得$ln{x}_{1}{x}_{2}-\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}=a({x}_{1}+{x}_{2})$,
两式相减得$ln\frac{{x}_{2}}{{x}_{1}}-\frac{{x}_{1}-{x}_{2}}{{x}_{1}{x}_{2}}=a({x}_{2}-{x}_{1})$,
即$\frac{ln\frac{{x}_{2}}{{x}_{1}}}{{x}_{2}-{x}_{1}}+\frac{1}{{x}_{1}{x}_{2}}=a$,
∴$ln{x}_{1}{x}_{2}-\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}=(\frac{ln\frac{{x}_{2}}{{x}_{1}}}{{x}_{2}-{x}_{1}}+\frac{1}{{x}_{1}{x}_{2}})({x}_{1}+{x}_{2})$,
即$ln{x}_{1}{x}_{2}-\frac{2({x}_{1}+{x}_{2})}{{x}_{1}{x}_{2}}=\frac{{x}_{1}+{x}_{2}}{{x}_{2}-{x}_{1}}•ln\frac{{x}_{2}}{{x}_{1}}$,
不妨令0<x1<x2,记t=$\frac{{x}_{2}}{{x}_{1}}$>1,
令F(t)=$lnt-\frac{2(t-1)}{t+1}$(t>1),则F′(t)=$\frac{(t-1)^{2}}{t(t+1)}$>0,
∴F(t)=$lnt-\frac{2(t-1)}{t+1}$在(1,+∞)上单调递增,则F(t)=$lnt-\frac{2(t-1)}{t+1}$>F(1)=0,
∴lnt>$\frac{2(t-1)}{t+1}$,则$ln\frac{{x}_{2}}{{x}_{1}}$>$\frac{2({x}_{2}-{x}_{1})}{{x}_{1}+{x}_{2}}$,
∴$ln{x}_{1}{x}_{2}-\frac{2({x}_{1}+{x}_{2})}{{x}_{1}{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{2}-{x}_{1}}•ln\frac{{x}_{2}}{{x}_{1}}$>2,
又$ln{x}_{1}{x}_{2}-\frac{2({x}_{1}+{x}_{2})}{{x}_{1}{x}_{2}}$<lnx1x2$-\frac{4\sqrt{{x}_{1}{x}_{2}}}{{x}_{1}{x}_{2}}$=$ln{x}_{1}{x}_{2}-\frac{4}{\sqrt{{x}_{1}{x}_{2}}}$=$2ln\sqrt{{x}_{1}{x}_{2}}-\frac{4}{\sqrt{{x}_{1}{x}_{2}}}$,
∴$2ln\sqrt{{x}_{1}{x}_{2}}-\frac{4}{\sqrt{{x}_{1}{x}_{2}}}$>2,即$ln\sqrt{{x}_{1}{x}_{2}}-\frac{2}{\sqrt{{x}_{1}{x}_{2}}}$>1,
令G(x)=lnx-$\frac{2}{x}$,则x>0时,G′(x)=$\frac{1}{x}+\frac{2}{{x}^{2}}$>0,
∴G(x)在(0,+∞)上单调递增,
又ln$\sqrt{2}e$-$\frac{2}{\sqrt{2}e}$=$\frac{1}{2}$ln2+1$-\frac{\sqrt{2}}{e}$≈0.85<1,
∴G($\sqrt{{x}_{1}{x}_{2}}$)=$ln\sqrt{{x}_{1}{x}_{2}}$$-\frac{2}{\sqrt{{x}_{1}{x}_{2}}}$>1>$ln\sqrt{2}e-\frac{2}{\sqrt{2}e}$,
则$\sqrt{{x}_{1}{x}_{2}}$$>\sqrt{2}e$,即x1•x2>2e2.
点评 本题主要考查了利用导数研究函数的单调性,考查函数构造、数学转化、放缩等数学思想方法,题目设置难度较大.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:选择题
| 女生 | 男生 | 合计 | |
| 喜欢吃甜食 | 8 | 4 | 12 |
| 不喜欢吃甜食 | 2 | 16 | 18 |
| 合计 | 10 | 20 | 30 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 有99.5%的把握认为性别对喜欢吃甜食无影响 | |
| B. | 有99.5%的把握认为性别对喜欢吃甜食有影响 | |
| C. | 有99.9%的把握认为性别对喜欢吃甜食无影响 | |
| D. | 有99.9%的把握认为性别对喜欢吃甜食有影响 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
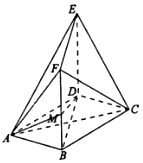 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,DE=2,M为线段BF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,DE=2,M为线段BF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,3) | C. | (3,+∞) | D. | (-∞,4-e) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
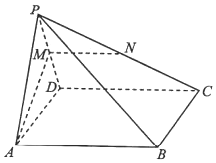 如图,在四棱锥P-ABCD中,底面ABCD是矩形,平面PAD⊥平面ABCD,AP=AD,M,N分别为棱PD,PC的中点.求证:
如图,在四棱锥P-ABCD中,底面ABCD是矩形,平面PAD⊥平面ABCD,AP=AD,M,N分别为棱PD,PC的中点.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
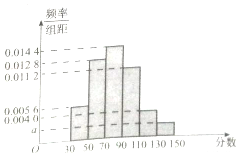 某市高二年级学生进行数学竞赛,竞赛分为初赛和决赛,规定成绩在110分及110分以上的学生进入决赛,110分以下的学生则被淘汰,现随机抽取500名学生的初赛成绩按[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]做成频率副本直方图,如图所示:(假设成绩在频率分布直方图中各段是均匀分布的)
某市高二年级学生进行数学竞赛,竞赛分为初赛和决赛,规定成绩在110分及110分以上的学生进入决赛,110分以下的学生则被淘汰,现随机抽取500名学生的初赛成绩按[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]做成频率副本直方图,如图所示:(假设成绩在频率分布直方图中各段是均匀分布的)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com