
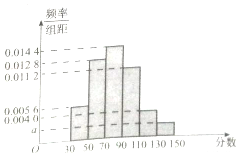
 某市高二年级学生进行数学竞赛,竞赛分为初赛和决赛,规定成绩在110分及110分以上的学生进入决赛,110分以下的学生则被淘汰,现随机抽取500名学生的初赛成绩按[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]做成频率副本直方图,如图所示:(假设成绩在频率分布直方图中各段是均匀分布的)
某市高二年级学生进行数学竞赛,竞赛分为初赛和决赛,规定成绩在110分及110分以上的学生进入决赛,110分以下的学生则被淘汰,现随机抽取500名学生的初赛成绩按[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]做成频率副本直方图,如图所示:(假设成绩在频率分布直方图中各段是均匀分布的)分析 (1)由题意和频率分布直方图列出方程,求出a,由此能求出这500名学生中进入决赛的人数,及进入决赛学生的平均分.
(2)由题意知抽取的6人中,成绩在[110,130)间的有4人,为A1,A2,A3,A4,成绩在[130,150)间的有2人,设为B1,B2,从6人中选取2人担任组长,利用列举法能求出组长中至少一名同学来自于高分组[130,150]的概率.
解答 解:(1)由题意和频率分布直方图,得:$\frac{500}{500×20}$=0.0144+0.0128+0.0112+0.0056+0.0040+a,
解得a=0.0020,
∴这500名学生中进入决赛的人数为:(0.0040+0.0020)×500×20=60,
进入决赛学生的平均分为:
40×0.0056×20+60×0.0128×20+80×0.0144×20+100×0.0112×20+120×0.0040×20+140×0.0020×20=80.48≈80.5,
∴这500名学生中有60人进入决赛,进入决赛学生的平均分为80.5分.
(2)由题意知抽取的6人中,成绩在[110,130)间的有4人,为A1,A2,A3,A4,
成绩在[130,150)间的有2人,设为B1,B2,
从6人中选取2人担任组长,基本事件总数n=${C}_{6}^{2}$=15,
其中至少一名同学来自高分组[130,150)的有:
(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(A4,B1),(A4,B2),(B1,B2),共9种情况,
∴组长中至少一名同学来自于高分组[130,150]的概率p=$\frac{9}{15}=\frac{3}{5}$.
点评 本题考查频率分布直方图、概率、列举法等基础知识,考查数据处理能力、运算求解能力,考查化归与转化思想、数形结合思想,是基础题.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 81π | B. | 9π | C. | $\frac{81π}{4}$ | D. | $\frac{9π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点P是线段BD1上的动点.当△PAC在平面DC1,BC1,AC上的正投影都为三角形时,将它们的面积分别记为S1,S2,S3.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点P是线段BD1上的动点.当△PAC在平面DC1,BC1,AC上的正投影都为三角形时,将它们的面积分别记为S1,S2,S3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com