
分析 (Ⅰ)当a=-1时,f'(x)=(2x-2)1nx+(x-2)-2x,由此利用导数的几何意义能求出f(x)在(1,f(1))处的切线方程.
(Ⅱ)令g(x)=f(x)-x-2=0,则$a=\frac{1-(x-2)1nx}{x}$令$h(x)=\frac{1-(x-2)1nx}{x}$,则h′(x)=$\frac{1-x-21nx}{x^2}$,令t(x)=1-x-21nx,则$t'(x)=-1-\frac{2}{x}=\frac{-x-2}{x}$,由此利用导数性质能求出当函数g(x)有且仅有一个零点时a的值.
(Ⅲ)当a=1,若e-2<x<e,g(x)≤m,只需证明g(x)max≤m,由g'(x)=(x-1)(3+21nx),求出$x={e^{-\frac{3}{2}}}$是g(x)的极大值点,由此能求出实数m的取值范围.
解答 解:(Ⅰ)当a=-1时,f(x)=(x2-2x)1nx-x2+2定义域(0,+∞),
f'(x)=(2x-2)1nx+(x-2)-2x,
∴f'(1)=-3,又f(1)=1,
∴f(x)在(1,f(1))处的切线方程3x+y-4=0.
(Ⅱ)令g(x)=f(x)-x-2=0,则(x2-2x)1nx+ax2+2=x+2
即$a=\frac{1-(x-2)1nx}{x}$
令$h(x)=\frac{1-(x-2)1nx}{x}$,
则$h'(x)=-\frac{1}{x^2}-\frac{1}{x}+\frac{2-21nx}{x^2}$=$\frac{1-x-21nx}{x^2}$,
令t(x)=1-x-21nx,则$t'(x)=-1-\frac{2}{x}=\frac{-x-2}{x}$,
∵x∈(0,+∞),∴t'(x)<0,
∴t(x)在(0,+∞)上是减函数,
又∵t(1)=h'(1)=0,
∴当0<x<1时,h'(x)>0,当x>1时,h'(x)<0,
∴h(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
∴h(x)max=h(1)=1>0,
又∵$h(\frac{1}{e})=1-e<0$,$h({e^2})=\frac{{5-2{e^2}}}{e^2}<0$,a>0
∴当函数g(x)有且仅有一个零点时,a=1
(Ⅲ)当a=1,g(x)=(x2-2x)1nx+x2-x,若e-2<x<e,g(x)≤m,
只需证明g(x)max≤m,g'(x)=(x-1)(3+21nx)
令g'(x)=0得x=1或$x={e^{-\frac{3}{2}}}$,又∵e-2<x<e,
∴函数g(x)在$({e^{-2}},{e^{-\frac{3}{2}}})$上单调递增,
在$({e^{-\frac{3}{2}}},1)$上单调递减,在(1,e)上单调递增,
即$x={e^{-\frac{3}{2}}}$是g(x)的极大值点,
又$g({e^{-\frac{3}{2}}})=-\frac{1}{2}{e^{-3}}+2{e^{-\frac{3}{2}}}$,g(e)=2e2-3e
∵$g({e^{-\frac{3}{2}}})=-\frac{1}{2}{e^{-3}}+2{e^{-\frac{3}{2}}}$$<2{e^{-\frac{3}{2}}}<2e<2e(e-\frac{3}{2})=g(e)$,
∴$g({e^{-\frac{3}{2}}})<g(e)$,∴m≥2e2-3e,
∴实数m的取值范围是(2e2-3e,+∞).
点评 本题考查函数的切线方程、实数的取值范围、导数的几何意义、导数性质、构造法等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,考查创新意识、应用意识,是中档题.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:解答题
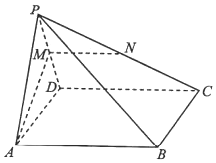 如图,在四棱锥P-ABCD中,底面ABCD是矩形,平面PAD⊥平面ABCD,AP=AD,M,N分别为棱PD,PC的中点.求证:
如图,在四棱锥P-ABCD中,底面ABCD是矩形,平面PAD⊥平面ABCD,AP=AD,M,N分别为棱PD,PC的中点.求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
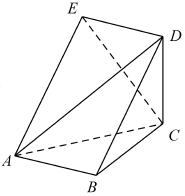 如图,五面体ABCDE中,四边形ABDE是菱形,△ABC是边长为2的正三角形,∠DBA=60°,$CD=\sqrt{3}$.
如图,五面体ABCDE中,四边形ABDE是菱形,△ABC是边长为2的正三角形,∠DBA=60°,$CD=\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
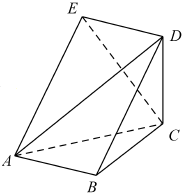 如图,五面体ABCDE中,四边形ABDE是菱形,△ABC是边长为2的正三角形,∠DBA=60°,$CD=\sqrt{3}$.
如图,五面体ABCDE中,四边形ABDE是菱形,△ABC是边长为2的正三角形,∠DBA=60°,$CD=\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
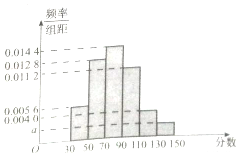 某市高二年级学生进行数学竞赛,竞赛分为初赛和决赛,规定成绩在110分及110分以上的学生进入决赛,110分以下的学生则被淘汰,现随机抽取500名学生的初赛成绩按[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]做成频率副本直方图,如图所示:(假设成绩在频率分布直方图中各段是均匀分布的)
某市高二年级学生进行数学竞赛,竞赛分为初赛和决赛,规定成绩在110分及110分以上的学生进入决赛,110分以下的学生则被淘汰,现随机抽取500名学生的初赛成绩按[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]做成频率副本直方图,如图所示:(假设成绩在频率分布直方图中各段是均匀分布的)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -5 | B. | -7 | C. | -9 | D. | -11 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com