
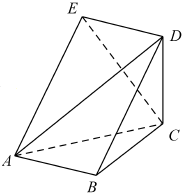
 如图,五面体ABCDE中,四边形ABDE是菱形,△ABC是边长为2的正三角形,∠DBA=60°,$CD=\sqrt{3}$.
如图,五面体ABCDE中,四边形ABDE是菱形,△ABC是边长为2的正三角形,∠DBA=60°,$CD=\sqrt{3}$.分析 (1)取AB的中点O,连OC,OD,证明:AB⊥平面DOC,即可证明DC⊥AB;
(2)取OD的中点H,连结CH,由VO-BCD=VB-OCD得点H到平面BCD的距离.
解答 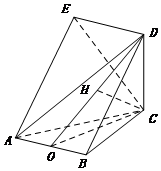 解:(1)证明:如图,取AB的中点O,连OC,OD,
解:(1)证明:如图,取AB的中点O,连OC,OD,
因为△ABC是边长为2的正三角形,所以$AB⊥OC,OC=\sqrt{3}$,
又四边形ABDE是菱形,∠DBA=60°,所以△DAB是正三角形,
所以$AB⊥OD,OD=\sqrt{3}$,
而OD∩OC=O,所以AB⊥平面DOC,
所以AB⊥CD;
(2)取OD的中点H,连结CH,
由(1)知OC=CD,所以AB⊥ODAB⊥平面DOC,所以平面DOC⊥平面ABD,
而平面DOC⊥平面ABD,平面DOC与平面ABD的交线为OD,
所以CH⊥平面ABD,即点H是D在平面ABD内的正投影,
设点H到平面BCD的距离为d,则点O到平面BCD距离为2d,
因为在△BCD中,$BC=BD=2,CD=\sqrt{3}$,
得${S_{△BCD}}=\frac{1}{2}•\sqrt{3}•\sqrt{{2^2}-{{(\frac{{\sqrt{3}}}{2})}^2}}=\frac{1}{2}•\sqrt{3}•\frac{{\sqrt{13}}}{2}$=$\frac{1}{2}•\sqrt{3}•\sqrt{{2^2}-{{(\frac{{\sqrt{3}}}{2})}^2}}=\frac{{\sqrt{39}}}{4}$,
在△OCD中,$OC=OD=CD=\sqrt{3}$,得${S_{△OCD}}=\frac{1}{2}•\sqrt{3}•\sqrt{3}•sin{60°}=\frac{{3\sqrt{3}}}{4}$,
所以由VO-BCD=VB-OCD得$\frac{1}{3}{S_{△BCD}}•d=\frac{1}{3}{S_{△OCD}}•OB$,
即$\frac{1}{3}•\frac{{\sqrt{39}}}{4}2d=\frac{1}{3}•\frac{{3\sqrt{3}}}{4}•1$,
解得$d=\frac{{3\sqrt{13}}}{26}$,所以H到平面BCD的距离$\frac{{3\sqrt{13}}}{26}$.
点评 本题考查线面垂直的判定与性质,考查H到平面BCD的距离,考查体积法的运用,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(1,-\frac{π}{2})$ | B. | (1,π) | C. | (0,-1) | D. | $(1,\frac{π}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 110 | B. | 10 | C. | 90 | D. | 80 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com