
分析 (1)求出g'(x)=ex-a,由a≤0和a>0分类讨论,由此能求出结果.
(2)当x>0时,$a≤\frac{e^x}{x}-x-\frac{1}{x}+1$令$h(x)=\frac{e^x}{x}-x-\frac{1}{x}+1(x>0)$,则$h'(x)=\frac{{{e^x}(x-1)-{x^2}+1}}{x^2}$令φ(x)=ex(x-1)-x2+1(x>0),则φ'(x)=x(ex-2),由此利用导数性质能求出实数a的取值范围.
解答 解:(1)∵g(x)=ex-ax-1,∴g'(x)=ex-a
①若a≤0,g'(x)>0,g(x)在(-∞,+∞)上单调递增;
②若a>0,当x∈(-∞,lna]时,g'(x)<0,g(x)单调递减;
当x∈(lna,+∞)时,g'(x)>0,g(x)单调递增.
(2)当x>0时,x2-x≤ex-ax-1,即$a≤\frac{e^x}{x}-x-\frac{1}{x}+1$
令$h(x)=\frac{e^x}{x}-x-\frac{1}{x}+1(x>0)$,则$h'(x)=\frac{{{e^x}(x-1)-{x^2}+1}}{x^2}$
令φ(x)=ex(x-1)-x2+1(x>0),则φ'(x)=x(ex-2)
当x∈(0,ln2)时,φ'(x)<0,φ(x)单调递减;
当x∈(ln2,+∞)时,φ'(x)>0,φ(x)单调递增
又φ(0)=0,φ(1)=0,
∴当x∈(0,1)时,φ(x)<0,即h'(x)<0,∴h(x)单调递减;
当x∈(0,+∞)时,φ(x)=(x-1)(ex-x-1>0,即h'(x)>0,
∴h(x)单调递增,
∴h(x)min=h(1)=e-1,
∴实数a的取值范围是(-∞,e-1].
点评 本题考查函数的单调性、实数的取值范围、导数性质、构造法等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,考查创新意识、应用意识,是中档题.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,由直线x=a,x=a+1(a>0),y=x2及x轴围成的曲边梯形的面积介于小矩形与大矩形的面积之间,即${a^2}<\int_a^{a+1}{{x^2}dx<{{(a+1)}^2}}$.类比之,若对?n∈N+,不等式$\frac{k}{n+1}+\frac{k}{n+2}+…+\frac{k}{2n}<1n4<\frac{k}{n}+\frac{k}{n+1}+…+\frac{k}{2n-1}$恒成立,则实数k等于2.
如图所示,由直线x=a,x=a+1(a>0),y=x2及x轴围成的曲边梯形的面积介于小矩形与大矩形的面积之间,即${a^2}<\int_a^{a+1}{{x^2}dx<{{(a+1)}^2}}$.类比之,若对?n∈N+,不等式$\frac{k}{n+1}+\frac{k}{n+2}+…+\frac{k}{2n}<1n4<\frac{k}{n}+\frac{k}{n+1}+…+\frac{k}{2n-1}$恒成立,则实数k等于2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
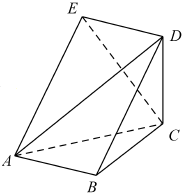 如图,五面体ABCDE中,四边形ABDE是菱形,△ABC是边长为2的正三角形,∠DBA=60°,$CD=\sqrt{3}$.
如图,五面体ABCDE中,四边形ABDE是菱形,△ABC是边长为2的正三角形,∠DBA=60°,$CD=\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com