
分析 (Ⅰ)利用等差数列的前n项和公式、等比数列性质,列出方程组,求出a1=2,d=2,由此能求出数列{an}的通项公式.
(Ⅱ)由${b_n}=\frac{1}{{({a_n}-1)({a_n}+1)}}$=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$,利用裂项求和法能证明Tn<$\frac{1}{2}$.
解答 解:(Ⅰ)∵Sn是等差数列{an}的前n项和,
公差d≠0,a5=10,且成等比数列,
∴由题知:$\left\{\begin{array}{l}{a_1}+4d=10\\{a_1}({a_1}+3d)={({a_1}+d)^2}\end{array}\right.$,
解得:a1=2,d=2,
故数列{an}的通项公式an=2n.
证明:(Ⅱ)∵${b_n}=\frac{1}{{({a_n}-1)({a_n}+1)}}$=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$,
∴Tn=b1+b2+…+bn=$\frac{1}{2}(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+…+\frac{1}{2n-1}-\frac{1}{2n+1})$=$\frac{1}{2}(1-\frac{1}{2n+1})<\frac{1}{2}$.
∴Tn<$\frac{1}{2}$.
点评 本题考查数列的通项公式的求法,考查等差数列的前n项和公式、能项公式、等比数列、裂项求和法等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,考查创新意识、应用意识,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,2] | B. | {0,1,2} | C. | (-1,2) | D. | {-1,0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
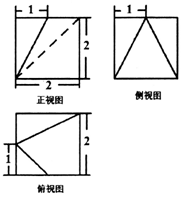 如图为一个多面体的三视图,则该多面体的体积为( )
如图为一个多面体的三视图,则该多面体的体积为( )| A. | $\frac{20}{3}$ | B. | 7 | C. | $\frac{22}{3}$ | D. | $\frac{23}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
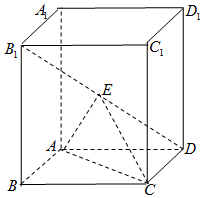 如图,四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,AA1⊥底面ABCD,E为B1D的中点.
如图,四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,AA1⊥底面ABCD,E为B1D的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
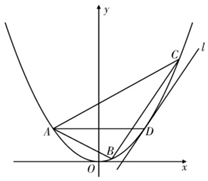 如图,已知A、B、C、D为抛物线E:x2=2py(p>0)上不同四点,其中A、D关于y轴对称,过点D作抛物线E的切线l和直线BC平行.
如图,已知A、B、C、D为抛物线E:x2=2py(p>0)上不同四点,其中A、D关于y轴对称,过点D作抛物线E的切线l和直线BC平行.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com