
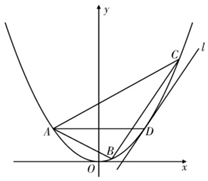
 如图,已知A、B、C、D为抛物线E:x2=2py(p>0)上不同四点,其中A、D关于y轴对称,过点D作抛物线E的切线l和直线BC平行.
如图,已知A、B、C、D为抛物线E:x2=2py(p>0)上不同四点,其中A、D关于y轴对称,过点D作抛物线E的切线l和直线BC平行.分析 (1)A(-x0,y0),D(x0,y0)B(x1,y1),C(x2,y2),证明kAC+kAB=$\frac{{x}_{2}-{x}_{0}}{2p}$+$\frac{{x}_{1}-{x}_{0}}{2p}$=0,由此能推导出∠BAC的角平分线在直线AD上.
(2)设∠BAD=∠CAD=α,则m=n=|AD|sinα,α=$\frac{π}{4}$,由此能推导出直线BC的方程.
解答 (1)证明:设A(-x0,y0),D(x0,y0)B(x1,y1),C(x2,y2),
∵y′=$\frac{x}{p}$,∴kBC=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$=$\frac{{x}_{1}+{x}_{2}}{2p}$=$\frac{{x}_{0}}{p}$,∴x1+x2=2x0,
kAC=$\frac{{x}_{2}-{x}_{0}}{2p}$.kAB=$\frac{{x}_{1}-{x}_{0}}{2p}$,
∴kAC+kAB=$\frac{{x}_{2}-{x}_{0}}{2p}$+$\frac{{x}_{1}-{x}_{0}}{2p}$=0,
所以直线AC和直线AB的倾斜角互补,所以∠BAD=∠CAD,
∴∠BAC的角平分线在直线AD上(6分)
(2)解:∠BAD=∠CAD=α
则m=n=|AD|sinα,∴sinα=$\frac{\sqrt{2}}{2}$,∴α=$\frac{π}{4}$,
∴直线AC的方程:y-$\frac{{{x}_{0}}^{2}}{4}$=x+x0,即y=x+$\frac{{{x}_{0}}^{2}}{4}$+x0,
把直线AC与抛物线方程x2=4y联立的x2-4x-4x0-x02=0∴-x0x2=-4x0-x02∴x2=x0+4
同理可得x1=x0-4,
∵-x0<x0-4<x0,∴x0>2,
∴S△ABC=$\frac{1}{3}\sqrt{2}(4+2{x}_{0})•\sqrt{2}(2{x}_{0}-4)$=$4({{x}_{0}}^{2}-4)$=128,
∴x0=6(10分)
∴B(2,1),kBC=3,∴lBC:3x-y-5=0(12分)
点评 本题考查直线和圆锥曲线的位置关系,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 顾 客 产 品 | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | a12 | a13 | a14 | a15 |
| A | 1 | 1 | 1 | 1 | 1 | ||||||||||
| B | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||
| C | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||
| D | 1 | 1 | 1 | 1 | 1 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(3)<f(-3) | B. | f(2)>f(-2) | C. | f(3)<f(2) | D. | 2f(3)>3f(2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
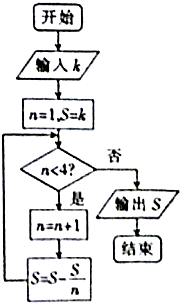 我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( )
我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( )| A. | 4.5 | B. | 6 | C. | 7.5 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,1) | B. | (-2,1) | C. | (-4,2) | D. | (-4,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{27}{16}$ | B. | $\frac{27}{8}$ | C. | $\frac{63}{4}$ | D. | $\frac{63}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com