
| �� �� �� Ʒ | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | a12 | a13 | a14 | a15 |
| A | 1 | 1 | 1 | 1 | 1 | ||||||||||
| B | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||
| C | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||
| D | 1 | 1 | 1 | 1 | 1 | 1 |
���� ��I��������ɵã���ƷA����������ԼΪ5��$\frac{300}{15}$��30��������
��II��һλ�˿����������ϣ������֣��²�Ʒ�ĸ���=$\frac{9}{15}$=$\frac{3}{5}$��
���мס��ҡ��������ڸó��й�������ǻ�õĵ��Ӻ���ĸ���Ϊ�Σ���Ρ�B��3��$\frac{3}{5}$����P����=k��=${∁}_{3}^{k}$$��\frac{2}{5}��^{3-k}��\frac{3}{5}��^{k}$���������X=2�Σ����ɵó���
��III�����ڹ˿���B���²�Ʒ�ĸ����������Ƽ������²�Ʒ��
��� �⣺��I��������ɵã�5��$\frac{300}{15}$��30=3000����������˲�ƷA����������ԼΪ3000��������
��II��һλ�˿����������ϣ������֣��²�Ʒ�ĸ���=$\frac{9}{15}$=$\frac{3}{5}$��
���мס��ҡ��������ڸó��й�������ǻ�õĵ��Ӻ���ĸ���Ϊ�Σ���Ρ�B��3��$\frac{3}{5}$����P����=k��=${∁}_{3}^{k}$$��\frac{2}{5}��^{3-k}��\frac{3}{5}��^{k}$��
�������X=2�εķֲ���Ϊ��
| X | 0 | 2 | 4 | 6 |
| P | $\frac{8}{125}$ | $\frac{36}{125}$ | $\frac{54}{125}$ | $\frac{27}{125}$ |
���� ���⿼���˶���ֲ��м�����ѧ��������������ʵļ��㹫ʽ��������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [0��2] | B�� | {0��1��2} | C�� | ��-1��2�� | D�� | {-1��0��1} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
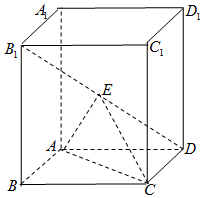 ��ͼ��������ABCD-A1B1C1D1�У�����ABCDΪ���Σ�AA1�͵���ABCD��EΪB1D���е㣮
��ͼ��������ABCD-A1B1C1D1�У�����ABCDΪ���Σ�AA1�͵���ABCD��EΪB1D���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 20 | B�� | 22 | C�� | 24 | D�� | 28 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
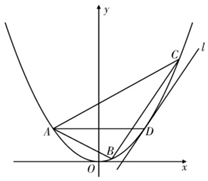 ��ͼ����֪A��B��C��DΪ������E��x2=2py��p��0���ϲ�ͬ�ĵ㣬����A��D����y��Գƣ�����D��������E������l��ֱ��BCƽ�У�
��ͼ����֪A��B��C��DΪ������E��x2=2py��p��0���ϲ�ͬ�ĵ㣬����A��D����y��Գƣ�����D��������E������l��ֱ��BCƽ�У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com