
分析 根据数列的递推公式可得数列{an}为公差为3的等差数列,再根据a2,a3,a5构成等比数列,即可求出通项公式.
解答 解:∵6Sn=an+12-9n,
当n=1时,6a1=a22-9
当n≥2时,6Sn-1=an2-9(n-1)
∴6an=an+12-9(n-1)-an2+9(n-1)
∴an+12=an2+6an+9=(an+3)2,
∵an>0,
∴an+1=an+3,
∴数列{an}为公差为3的等差数列,
∴an=a1+3(n-1),
∵a2,a3,a5构成等比数列,
∴a32=a2•a5,
∴(a1+6)2=(a1+3)(a1+12)
解得a1=0,
∴an={an}3n-3,
∴a2=3,
∴满足6a1=a22-9,
∴an=3n-3,
故答案为:3n-3
点评 本题考查了数列的递推公式和和通项公式的求法,考查了学生分析问题解决问题的能力,属于中档题


科目:高中数学 来源: 题型:解答题
| 顾 客 产 品 | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | a12 | a13 | a14 | a15 |
| A | 1 | 1 | 1 | 1 | 1 | ||||||||||
| B | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||
| C | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||
| D | 1 | 1 | 1 | 1 | 1 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
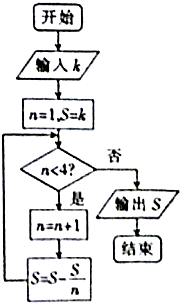 我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( )
我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( )| A. | 4.5 | B. | 6 | C. | 7.5 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,1) | B. | (-2,1) | C. | (-4,2) | D. | (-4,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{30}{17}$ | C. | $\frac{47}{17}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,6) | B. | (-1,6) | C. | (-$\frac{8}{3}$,-1] | D. | (-$\frac{8}{3}$,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{27}{16}$ | B. | $\frac{27}{8}$ | C. | $\frac{63}{4}$ | D. | $\frac{63}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2)∪(2,+∞) | B. | (-∞,-,4)∪(4,+∞) | C. | (-2,2) | D. | (-4,4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com