
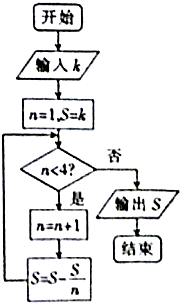
 我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( )
我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( )| A. | 4.5 | B. | 6 | C. | 7.5 | D. | 9 |
分析 模拟程序的运行,依次写出每次循环得到的n,S的值,当n=4时,不满足条件n<4,退出循环,输出S的值为$\frac{k}{4}$,即可解得k的值.
解答 解:模拟程序的运行,可得
n=1,S=k
满足条件n<4,执行循环体,n=2,S=k-$\frac{k}{2}$=$\frac{k}{2}$,
满足条件n<4,执行循环体,n=3,S=$\frac{k}{2}$-$\frac{\frac{k}{2}}{3}$=$\frac{k}{3}$,
满足条件n<4,执行循环体,n=4,S=$\frac{k}{3}$-$\frac{\frac{k}{3}}{4}$=$\frac{k}{4}$,
此时,不满足条件n<4,退出循环,输出S的值为$\frac{k}{4}$,
由题意可得:$\frac{k}{4}$=1.5,解得:k=6.
故选:B.
点评 算法和程序框图是新课标新增的内容,在近两年的新课标地区高考都考查到了,这启示我们要给予高度重视,属于基础题.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源: 题型:解答题
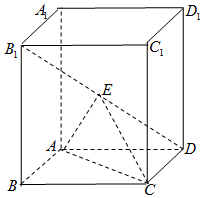 如图,四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,AA1⊥底面ABCD,E为B1D的中点.
如图,四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,AA1⊥底面ABCD,E为B1D的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
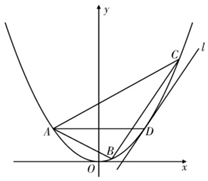 如图,已知A、B、C、D为抛物线E:x2=2py(p>0)上不同四点,其中A、D关于y轴对称,过点D作抛物线E的切线l和直线BC平行.
如图,已知A、B、C、D为抛物线E:x2=2py(p>0)上不同四点,其中A、D关于y轴对称,过点D作抛物线E的切线l和直线BC平行.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=f(-x)•e-x-1 | B. | y=f(x)•ex+1 | C. | y=f(x)•ex-1 | D. | y=f(-x)•ex+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -4 | C. | -8 | D. | -16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com