
���� ��1����ȥ����t��ֱ��l����ͨ���̣����ü�������ֱ�����껥������������C��ֱ�����귽�̣�
��2�����M��P��ֱ�����꣬������|PM|��ֵ��
��� �⣺��1����ֱ֪��l�IJ���������$\left\{\begin{array}{l}x=\frac{1}{2}t\\ y=3+\frac{{\sqrt{3}}}{2}t\end{array}\right.$��tΪ����������ͨ����Ϊy=$\sqrt{3}x$+3��
����C�ļ����귽���Ǧ�cos2��=4sin�ȣ���Ϊ��2cos2��=4��sin�ȣ�
��x2=4y������5�֣�
��2����ֱ���������߷��̣���ȥy��x2-4$\sqrt{3}$x-12=0����6�֣�
��A��x1��y1����B��x2��y2������AB���е�M��2$\sqrt{3}$��9������8�֣�
�ֵ�P��ֱ������Ϊ��2$\sqrt{3}$��6��������9�֣�
����|PM|=3����10�֣�
���� ���⿼����ֱ�����귽�̻�Ϊ�������̡������귽�̻�Ϊֱ�����귽�̡�ֱ���������ߵ�λ�ù�ϵ��������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | f��3����f��-3�� | B�� | f��2����f��-2�� | C�� | f��3����f��2�� | D�� | 2f��3����3f��2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
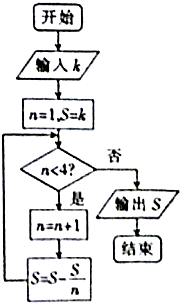 �ҹ��Ŵ���ѧ�������������������������⣺�����������ף���֪������ǰ��ȡ�룬��������ȡһ�������ķ�ȡһ������һ���������ʣ����Σ�����ͼ�ǽ��������ij����ͼ��ִ�иó����ͼ���������S=1.5����λ��������������k��ֵΪ��������
�ҹ��Ŵ���ѧ�������������������������⣺�����������ף���֪������ǰ��ȡ�룬��������ȡһ�������ķ�ȡһ������һ���������ʣ����Σ�����ͼ�ǽ��������ij����ͼ��ִ�иó����ͼ���������S=1.5����λ��������������k��ֵΪ��������| A�� | 4.5 | B�� | 6 | C�� | 7.5 | D�� | 9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
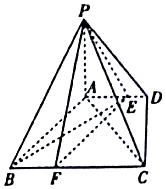 ��ͼ������P-ABCD�У�PA�͵���ABCD������ABCD��ֱ�����Σ���ADC=90�㣬AD��BC��AB��AC��AB=AC=$\sqrt{2}$����E��AD�ϣ���AE=2ED��
��ͼ������P-ABCD�У�PA�͵���ABCD������ABCD��ֱ�����Σ���ADC=90�㣬AD��BC��AB��AC��AB=AC=$\sqrt{2}$����E��AD�ϣ���AE=2ED���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-3��1�� | B�� | ��-2��1�� | C�� | ��-4��2�� | D�� | ��-4��3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | $\frac{30}{17}$ | C�� | $\frac{47}{17}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com