练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．在复平面内，复数$\frac{3+4i}{i}$对应的点的坐标为（4，-3）．

    分析 利用复数的运算法则、几何意义即可得出．

    解答 解：复数$\frac{3+4i}{i}$=$\frac{-i（3+4i）}{-i•i}$=-3i+4对应的点的坐标为（4，-3）．
    故答案为：（4，-3）．

    点评 本题考查了复数的运算法则、几何意义，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    13．某校高三特长班的一次月考数学成绩的茎叶图和频率分布直方图1都受到不同程度的损坏，但可见部分如图2，据此解答如下问题：

    （Ⅰ）求分数在[70，80）之间的频数，并计算频率分布直方图中[70，80）间的矩形的高；
    （Ⅱ）若要从分数在[50，70）之间的试卷中任取两份分析学生失分情况，在抽取的试卷中，求至少有一份在[50，60）之间的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

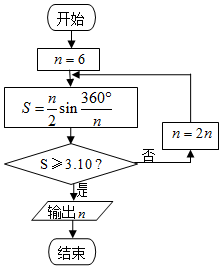    14．公元263年左右，我国古代数学家刘徽用圆内接正多边形的面积去逼近圆的面积求圆周率π，刘徽称这个方法为“割圆术”，并且把“割圆术”的特点概括为“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”下图是根据刘徽的“割圆术”思想设计的一个程序框图．若运行该程序，则输出的n的值为：（参考数据：$\sqrt{3}$≈1.732，sin15°≈0.2588，sin7.5°≈0.1305）（　　）
    A．48B．36C．30D．24

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{20}$=1（a＞0）的一条渐近线方程为y=2x，则该双曲线的焦距为10．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知函数f（x）=sin2xcos$\frac{3π}{5}-cos2xsin\frac{3π}{5}$．
    （Ⅰ）求f（x）的最小正周期和对称轴的方程；
    （Ⅱ）求f（x）在区间$[0，\frac{π}{2}]$上的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．某社区超市购进了A，B，C，D四种新产品，为了解新产品的销售情况，该超市随机调查了15位顾客（记为ai，i=1，2，3，…，15）购买这四种新产品的情况，记录如下（单位：件）：
    顾
    客
    产
    品    		a1a2a3a4a5a6a7a8a9a10a11a12a13a14a15
    A11111
    B11111111
    C1111111
    D111111
    （Ⅰ）若该超市每天的客流量约为300人次，一个月按30天计算，试估计产品A的月销售量（单位：件）；
    （Ⅱ）为推广新产品，超市向购买两种以上（含两种）新产品的顾客赠送2元电子红包．现有甲、乙、丙三人在该超市购物，记他们获得的电子红包的总金额为X，求随机变量X的分布列和数学期望；
    （Ⅲ）若某顾客已选中产品B，为提高超市销售业绩，应该向其推荐哪种新产品？（结果不需要证明）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．若实数x，y满足约束条件$\left\{\begin{array}{l}x≥0\;\\ y≤x\;\\ x+y+a≤0\;\end{array}\right.$且z=x+3y的最大值为4，则实数a的值为-2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．已知函数f（x）的导函数f′（x），满足（x-1）[xf′（x）-f（x）]＞0，则下列关于f（x）的命题正确的是（　　）
    A．f（3）＜f（-3）B．f（2）＞f（-2）C．f（3）＜f（2）D．2f（3）＞3f（2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知实数x，y满足$\left\{\begin{array}{l}{3x-y-7≥0}\\{5x-4y≤0}\\{y≤10}\end{array}\right.$，则$\frac{y+x}{x}$的最大值为（　　）
    A．1B．$\frac{30}{17}$C．$\frac{47}{17}$D．2

    查看答案和解析>>

    同步练习册答案