
分析 (1)通过讨论f(x)和F(x)的单调性,得到F(x)的最小值,问题转化为关于a的不等式,解出即可;
(2)将所要证明的式子变形,建立一个函数,求导后再建立一个新的函数,再求导.需要用到两次求导.再来通过最值确定正负号,再来确实原函数的单调性.
解答 解:(1)由题意得:x>0,而F(x)的最小值是F($\sqrt{2}$)=2$\sqrt{2}$,
而f(x)=lnx-a在(0,+∞)递增,
故只需f($\sqrt{2}$)<2$\sqrt{2}$即可,
即ln$\sqrt{2}$-a<2$\sqrt{2}$,
解得:a>ln$\sqrt{2}$-2$\sqrt{2}$;
若函数f(x)=lnx-a(a∈R)与函数F(x)=x+$\frac{2}{x}$的图象没有交点,
(2)原式等价于xlnx+a+e-2-ax≥0在(0,+∞)上恒成立.
令g(x)=xlnx+a+e-2-ax.
∵g′(x)=lnx+1-a
令g′(x)=0,得x=ea-1
①0<x<ea-1时,g′(x)<0,g(x)单调递减
②ea-1<x时,g′(x)>0,g(x)单调递增
∴g(x)的最小值为g(ea-1)=(a-1)ea-1+a+e-2-aea-1=a+e-2-ea-1.
令t(x)=x+e-2-ea-1.∵t′(x)=1-ea-1.
令t′(x)=0.得x=1.且
③0<x<1时,t′(x)>0,t(x)单调递增
④1<x时,t′(x)<0,t(x)单调递减
∴当a∈(0,1)时,g(x)的最小值t(a)>t(0)=e-2-$\frac{1}{e}$=$\frac{e(e-2)-1}{e}$>0.
当a∈[1,+∞)时,g(x)的最小值为t(a)=a+e-2-ea-1≥0=t(2).
∴a∈[1,2].
综上得:a∈(0,2].
点评 本题主要考查函数求导来寻找单调区间及最值.尤其是第二问需要对函数求导后再建立一个新的函数求导,这也是一个常见类型.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 110 | B. | 10 | C. | 90 | D. | 80 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
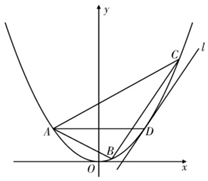 如图,已知A、B、C、D为抛物线E:x2=2py(p>0)上不同四点,其中A、D关于y轴对称,过点D作抛物线E的切线l和直线BC平行.
如图,已知A、B、C、D为抛物线E:x2=2py(p>0)上不同四点,其中A、D关于y轴对称,过点D作抛物线E的切线l和直线BC平行.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=f(-x)•e-x-1 | B. | y=f(x)•ex+1 | C. | y=f(x)•ex-1 | D. | y=f(-x)•ex+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com