
分析 根据题意,令g(x)=xf(x),则a=g(40.2),b=g(log43),c=f(log4$\frac{1}{16}$),由函数的奇偶性定义分析可得g(x)为偶函数,对g(x)求导可得g′(x)>0,即g(x)在(0,+∞)上为增函数,比较可得|log4$\frac{1}{16}$|>|40.2|>|log43|,结合函数的单调性分析可得答案.
解答 解:根据题意,令g(x)=xf(x),则a=g(40.2),b=g(log43),c=f(log4$\frac{1}{16}$)
有g(-x)=(-x)f(-x)=(-x)[-f(x)]=xf(x),则g(x)为偶函数,
又由g′(x)=(x)′f(x)+xf'(x)=f(x)+xf'(x),
又由当x∈(0,+∞)时,都有不等式f(x)+xf'(x)>0成立,
则当x∈(0,+∞)时,有g′(x)>0,即g(x)在(0,+∞)上为增函数,
分析可得|log4$\frac{1}{16}$|>|40.2|>|log43|,
则有c>a>b;
故答案为:c>a>b.
点评 本题考查函数的导数与单调性的关系,涉及函数奇偶性的性质应用,关键是构造函数g(x)=xf(x).


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 110 | B. | 10 | C. | 90 | D. | 80 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
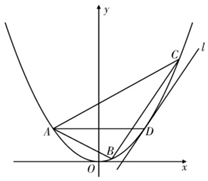 如图,已知A、B、C、D为抛物线E:x2=2py(p>0)上不同四点,其中A、D关于y轴对称,过点D作抛物线E的切线l和直线BC平行.
如图,已知A、B、C、D为抛物线E:x2=2py(p>0)上不同四点,其中A、D关于y轴对称,过点D作抛物线E的切线l和直线BC平行.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=f(-x)•e-x-1 | B. | y=f(x)•ex+1 | C. | y=f(x)•ex-1 | D. | y=f(-x)•ex+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{31\sqrt{2}}{2}$+31 | B. | 31$\sqrt{2}$+31 | C. | 80 | D. | $\frac{5\sqrt{2}}{2}$+80 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com