练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
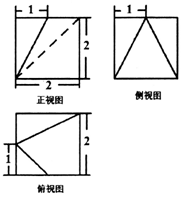
    2．如图为一个多面体的三视图，则该多面体的体积为（　　）
    A．$\frac{20}{3}$B．7C．$\frac{22}{3}$D．$\frac{23}{3}$

    分析 如图所示，由已知三视图可知：该几何体为正方体去掉两个倒立的三棱锥．利用体积计算公式即可得出．

    解答 解：如图所示，由已知三视图可知：该几何体为正方体去掉两个倒立的三棱锥．
    ∴该多面体的体积V=23-$\frac{1}{3}×\frac{1}{2}×1×2×2$-$\frac{1}{3}×\frac{1}{2}×{1}^{2}×2$
    =7．
    故选：B．

    点评 本题考查了正方体与三棱锥的三视图与体积计算公式，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    12．某人随机播放甲、乙、丙、丁4首歌曲中的2首，则甲、乙2首歌曲至少有1首被播放的概率是$\frac{5}{6}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．某校高三特长班的一次月考数学成绩的茎叶图和频率分布直方图1都受到不同程度的损坏，但可见部分如图2，据此解答如下问题：

    （Ⅰ）求分数在[70，80）之间的频数，并计算频率分布直方图中[70，80）间的矩形的高；
    （Ⅱ）若要从分数在[50，70）之间的试卷中任取两份分析学生失分情况，在抽取的试卷中，求至少有一份在[50，60）之间的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．如图所示，由直线x=a，x=a+1（a＞0），y=x2及x轴围成的曲边梯形的面积介于小矩形与大矩形的面积之间，即${a^2}＜\int_a^{a+1}{{x^2}dx＜{{（a+1）}^2}}$．类比之，若对?n∈N+，不等式$\frac{k}{n+1}+\frac{k}{n+2}+…+\frac{k}{2n}＜1n4＜\frac{k}{n}+\frac{k}{n+1}+…+\frac{k}{2n-1}$恒成立，则实数k等于2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．已知函数$f（x）=\left\{\begin{array}{l}2a-x，x≤0\\{log_a}x，x＞0\end{array}\right.$（a＞0且a≠1），若f（f（1））=1，则a=$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．设Sn是等差数列{an}的前n项和，若公差d≠0，a5=10，且成等比数列．
    （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）设bn=$\frac{1}{{（{a_n}-1）（{a_n}+1）}}$，Tn=b1+b2+…+bn，求证：Tn＜$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

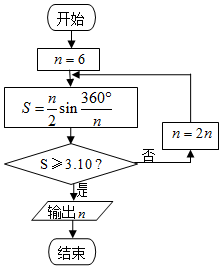    14．公元263年左右，我国古代数学家刘徽用圆内接正多边形的面积去逼近圆的面积求圆周率π，刘徽称这个方法为“割圆术”，并且把“割圆术”的特点概括为“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”下图是根据刘徽的“割圆术”思想设计的一个程序框图．若运行该程序，则输出的n的值为：（参考数据：$\sqrt{3}$≈1.732，sin15°≈0.2588，sin7.5°≈0.1305）（　　）
    A．48B．36C．30D．24

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{20}$=1（a＞0）的一条渐近线方程为y=2x，则该双曲线的焦距为10．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．已知函数f（x）的导函数f′（x），满足（x-1）[xf′（x）-f（x）]＞0，则下列关于f（x）的命题正确的是（　　）
    A．f（3）＜f（-3）B．f（2）＞f（-2）C．f（3）＜f（2）D．2f（3）＞3f（2）

    查看答案和解析>>

    同步练习册答案