
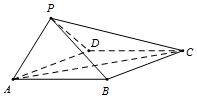
 如图,菱形ABCD与等边△PAD所在的平面相互垂直,AD=2,∠DAB=60°.
如图,菱形ABCD与等边△PAD所在的平面相互垂直,AD=2,∠DAB=60°.分析 (Ⅰ)取AD中点O,连结OP、OB、BD,推导出AD⊥平面POB,由此能证明AD⊥PB.
(Ⅱ)法一:设点C到平面PAB的距离为h,由VC-PAB=VP-ABC,能求出三棱锥C-PAB的高.
法二:以O为原点,OA为x轴,OB为y轴,OP为z轴,建立空间直角坐标系,利用向量法能求出三棱锥C-PAB的高.
解答 证明:(Ⅰ)取AD中点O,连结OP、OB、BD,
∵菱形ABCD与等边△PAD所在的平面相互垂直,
AD=2,∠DAB=60°.
∴OP⊥AD,BO⊥AD,
∵OP∩BO=O,∴AD⊥平面POB,
∵PB?平面POB,∴AD⊥PB.
解:(Ⅱ)法一:∵菱形ABCD与等边△PAD所在的平面相互垂直,AD=2,∠DAB=60°.
∴BO=PO=$\sqrt{4-1}$=$\sqrt{3}$,PB=$\sqrt{3+3}$=$\sqrt{6}$,
∴${S}_{△PAB}=\frac{1}{2}×\sqrt{6}×\sqrt{4-\frac{6}{4}}$=$\frac{\sqrt{15}}{2}$,
${S}_{△ABC}={S}_{△ABD}=\frac{1}{2}×2×2×sin60°$=$\sqrt{3}$.
设点C到平面PAB的距离为h,
∵VC-PAB=VP-ABC,
∴$\frac{1}{3}×{S}_{△PAB}×h=\frac{1}{3}×{S}_{△ABC}×PO$,
∴h=$\frac{{S}_{△ABC}×PO}{{S}_{△PAB}}$=$\frac{\sqrt{3}×\sqrt{3}}{\frac{\sqrt{15}}{2}}$=$\frac{2\sqrt{15}}{5}$.
∴三棱锥C-PAB的高为$\frac{2\sqrt{15}}{5}$.
法二:以O为原点,OA为x轴,OB为y轴,OP为z轴,建立空间直角坐标系,
则A(1,0,0),B(0,$\sqrt{3}$,0),C(-2,$\sqrt{3}$,0),P(0,0,$\sqrt{3}$),
$\overrightarrow{PA}$=(1,0,-$\sqrt{3}$),$\overrightarrow{PB}$=(0,$\sqrt{3}$,-$\sqrt{3}$),$\overrightarrow{PC}$=(-2,$\sqrt{3}$,-$\sqrt{3}$),
设平面PAB的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{PA}=x-\sqrt{3}z=0}\\{\overrightarrow{n}•\overrightarrow{PB}=\sqrt{3}y-\sqrt{3}z=0}\end{array}\right.$,
取z=1,得$\overrightarrow{n}$=($\sqrt{3},1,1$),
∴点C到平面PAB的距离h=$\frac{|\overrightarrow{PC}•\overrightarrow{n}|}{|\overrightarrow{n}|}$=$\frac{2\sqrt{3}}{\sqrt{5}}$=$\frac{2\sqrt{15}}{5}$,
∴三棱锥C-PAB的高为$\frac{2\sqrt{15}}{5}$.
点评 本题考查线线垂直的证明,考查几何体的高的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
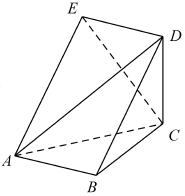 如图,五面体ABCDE中,四边形ABDE是菱形,△ABC是边长为2的正三角形,∠DBA=60°,$CD=\sqrt{3}$.
如图,五面体ABCDE中,四边形ABDE是菱形,△ABC是边长为2的正三角形,∠DBA=60°,$CD=\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
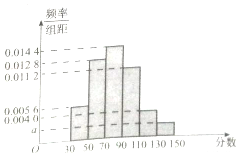 某市高二年级学生进行数学竞赛,竞赛分为初赛和决赛,规定成绩在110分及110分以上的学生进入决赛,110分以下的学生则被淘汰,现随机抽取500名学生的初赛成绩按[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]做成频率副本直方图,如图所示:(假设成绩在频率分布直方图中各段是均匀分布的)
某市高二年级学生进行数学竞赛,竞赛分为初赛和决赛,规定成绩在110分及110分以上的学生进入决赛,110分以下的学生则被淘汰,现随机抽取500名学生的初赛成绩按[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]做成频率副本直方图,如图所示:(假设成绩在频率分布直方图中各段是均匀分布的)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -5 | B. | -7 | C. | -9 | D. | -11 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com