
分析 掷两次骰子分别得到的点数m,n,组成的向量(m,n)个数为36个,只需列举出满足条件的即可.
解答 解:后连掷两次骰子分别得到点数m,n,所组成的向量(m,n)的个数共有36种
由于向量(m,n)与向量(1,-1)的夹角θ为锐角,∴(m,n)•(1,-1)>0,
即m>n,满足题意的情况如下:
当m=2时,n=1;
当m=3时,n=1,2;
当m=4时,n=1,2,3;
当m=5时,n=1,2,3,4;
当m=6时,n=1,2,3,4,5;共有15种,
故所求事件的概率为:$\frac{15}{36}$=$\frac{5}{12}$,
故答案为:$\frac{5}{12}$.
点评 本题考查等可能事件的概率,得出m>n并正确列举是解决问题的关键,属基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,3) | C. | (3,+∞) | D. | (-∞,4-e) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
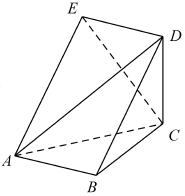 如图,五面体ABCDE中,四边形ABDE是菱形,△ABC是边长为2的正三角形,∠DBA=60°,$CD=\sqrt{3}$.
如图,五面体ABCDE中,四边形ABDE是菱形,△ABC是边长为2的正三角形,∠DBA=60°,$CD=\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
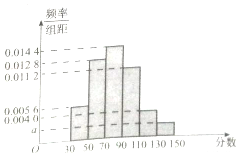 某市高二年级学生进行数学竞赛,竞赛分为初赛和决赛,规定成绩在110分及110分以上的学生进入决赛,110分以下的学生则被淘汰,现随机抽取500名学生的初赛成绩按[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]做成频率副本直方图,如图所示:(假设成绩在频率分布直方图中各段是均匀分布的)
某市高二年级学生进行数学竞赛,竞赛分为初赛和决赛,规定成绩在110分及110分以上的学生进入决赛,110分以下的学生则被淘汰,现随机抽取500名学生的初赛成绩按[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]做成频率副本直方图,如图所示:(假设成绩在频率分布直方图中各段是均匀分布的)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com