
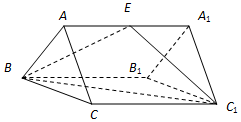
 如图:三棱柱ABC-A1B1C1的所有棱长均相等,AA1⊥平面ABC,E为AA1的中点.
如图:三棱柱ABC-A1B1C1的所有棱长均相等,AA1⊥平面ABC,E为AA1的中点.分析 (1)连接CB1交BC1于点O,连接EC,EB1,推导出EO⊥CB1,EO⊥BC1,从而EO⊥平面BCC1B1,由此能证明平面EBC1⊥平面BCC1B1.
(2)取A1B1的中点为H,连接C1H、BH,推导出C1H⊥平面BB1A1A,则∠C1BH为直线BC1与平面BB1A1A所成的角,由此能求出直线BC1与平面BB1A1A所成角的正弦值.
解答  证明:(1)如图1,连接CB1交BC1于点O,则O为CB1与BC1的中点,
证明:(1)如图1,连接CB1交BC1于点O,则O为CB1与BC1的中点,
连接EC,EB1,
依题意有;EB=EC1=EC=EB1,…(2分)
∴EO⊥CB1,EO⊥BC1,
∵CB1∩BC1=O,∴EO⊥平面BCC1B1,
∵OE⊆平面BC1E,∴平面EBC1⊥平面BCC1B1.…(5分)
解:(2)如图2,取A1B1的中点为H,连接C1H、BH,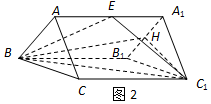
∵AA1⊥平面ABC,∴平面A1B1C1⊥平面BB1A1A,
平面A1B1C1∩平面BB1A1A=A1B1,
又∵A1C1=B1C1,H为A1B1的中点,
∴C1H⊥A1B1,∴C1H⊥平面BB1A1A,
则∠C1BH为直线BC1与平面BB1A1A所成的角.…(8分)
令棱长为2a,则C1H=$\sqrt{3}a$,BC1=$2\sqrt{2}a$,
∴$sin∠{C_1}BH=\frac{{\sqrt{3}a}}{{2\sqrt{2}a}}=\frac{{\sqrt{6}}}{4}$
所以直线BC1与平面BB1A1A所成角的正弦值为$\frac{{\sqrt{6}}}{4}$.…(12分)
点评 本题考查面面垂直的证明,考查线面角的正弦值的求法,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
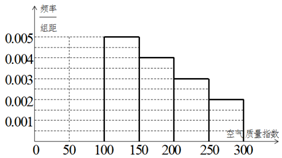 某中学环保社团参照国家环境标准,制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):
某中学环保社团参照国家环境标准,制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):| 空气质量指数 | (0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] |
| 空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
| 空气质量指数 | 频数 | 频率 |
| (0,50] | x | a |
| (50,100] | y | b |
| (100,150] | 25 | 0.25 |
| (150,200] | 20 | 0.2 |
| (200,250] | 15 | 0.15 |
| (250,300] | 10 | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若0<α<$\frac{π}{2}$,则sinα<tanα | |
| B. | 若α是第二象限角,则$\frac{α}{2}$为第一象限或第三象限角 | |
| C. | 若角α的终边过点P(3k,4k)(k≠0),则sinα=$\frac{4}{5}$ | |
| D. | 若扇形的周长为6,半径为2,则其中心角的大小为1弧度 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$-1 | B. | $\sqrt{2}$+1 | C. | 8$\sqrt{2}$-8 | D. | 2$\sqrt{2}$-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 52 | B. | $2\sqrt{13}$ | C. | 100-48$\sqrt{3}$ | D. | $\sqrt{100-48\sqrt{3}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
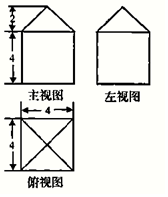
| A. | 96+16$\sqrt{2}$cm2 | B. | 80+16$\sqrt{2}$cm2 | C. | 96+32$\sqrt{2}$cm2 | D. | 80+32$\sqrt{2}$cm2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com