
| A. | 若0<α<$\frac{π}{2}$,则sinα<tanα | |
| B. | 若α是第二象限角,则$\frac{α}{2}$为第一象限或第三象限角 | |
| C. | 若角α的终边过点P(3k,4k)(k≠0),则sinα=$\frac{4}{5}$ | |
| D. | 若扇形的周长为6,半径为2,则其中心角的大小为1弧度 |
分析 利用任意角的三角函数的定义,象限角的定义,判断各个选项是否正确,从而得出结论.
解答 解:若0<α<$\frac{π}{2}$,则sinα<tanα=$\frac{sinα}{cosα}$,故A正确;
若α是第二象限角,即α(2kπ,2kπ+π),k∈Z,则$\frac{α}{2}$∈(kπ,kπ+$\frac{π}{2}$),为第一象限或第三象限,故B正确;
若角α的终边过点P(3k,4k)(k≠0),则sinα=$\frac{4k}{\sqrt{{9k}^{2}+1{6k}^{2}}}$=$\frac{4k}{5|k|}$,不一定等于$\frac{4}{5}$,故C不正确;
若扇形的周长为6,半径为2,则弧长=6-2×2=2,其中心角的大小为$\frac{2}{2}$=1弧度,
故选:C.
点评 本题主要考查任意角的三角函数的定义,象限角的判定,属于基础题.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1-ln2}{8},\frac{1-ln2}{6})∪(\frac{ln2-1}{6},\frac{ln2-1}{8})$ | B. | $(\frac{ln2-1}{6},\frac{ln2-1}{8})$ | ||
| C. | $(\frac{1-ln2}{8},\frac{1-ln2}{6})$ | D. | $(\frac{1-ln2}{8},\frac{ln2-1}{6})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=log${\;}_{\frac{1}{2}}$|x| | B. | y=x${\;}^{\frac{1}{2}}$ | C. | y=$\frac{{{2^x}+{2^{-x}}}}{2}$ | D. | y=lg$\frac{2-x}{2+x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | c<a<b | C. | b<c<a | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
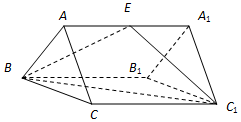 如图:三棱柱ABC-A1B1C1的所有棱长均相等,AA1⊥平面ABC,E为AA1的中点.
如图:三棱柱ABC-A1B1C1的所有棱长均相等,AA1⊥平面ABC,E为AA1的中点.查看答案和解析>>
科目:高中数学 来源:2016-2017学年浙江普通高校招生学业水平考试数学试卷(解析版) 题型:选择题
在空间中,下列命题正确的是( )
A.经过三个点有且只有一个平面
B.经过一个点和一条直线有且只有一个平面
C.经过一个点且与一条直线平行的平面有且只有一个
D.经过一个点且与一条直线垂直的平面有且只有一个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com