Question

5．在研究函数 f （ x ）=$\sqrt{{x^2}+4}$-$\sqrt{{x^2}-12x+40}$的性质时，某同学受两点间距离公式启发，将f（x）变形为f（x）=$\sqrt{（x-0{）^2}+（0-2{）^2}}$-$\sqrt{（x-6{）^2}+（0-2{）^2}}$，并给出关于函数f（x）以下五个描述：
①函数 f（x）的图象是中心对称图形； 
②函数 f（x）的图象是轴对称图形；
③函数 f（x）在[0，6]上是增函数；
④函数 f（x）没有最大值也没有最小值；
⑤无论m为何实数，关于x的方程 f（x）-m=0都有实数根．
其中描述正确的是①③④．

Answer 1

分析 函数 f （ x ）=$\sqrt{{x^2}+4}$-$\sqrt{{x^2}-12x+40}$=$\sqrt{（x-0{）^2}+（0-2{）^2}}$-$\sqrt{（x-6{）^2}+（0-2{）^2}}$，如图表示点P（x，0）到点A（0，2）的距离|PA|与到点B（6，2）的距离|PB|之差；结合图形可知，在x=3处，f（x）=0，-6＜PA-PB＜6
∴函数 f（x）的图象是中心对称图形，对称中心为（3，0），即可判断．

解答 解：函数 f （ x ）=$\sqrt{{x^2}+4}$-$\sqrt{{x^2}-12x+40}$=$\sqrt{（x-0{）^2}+（0-2{）^2}}$-$\sqrt{（x-6{）^2}+（0-2{）^2}}$，如图表示点P（x，0）到点A（0，2）的距离|PA|与到点B（6，2）的距离|PB|之差；结合图形可知，在x=3处，f（x）=0，-6＜PA-PB＜6
∴函数 f（x）的图象是中心对称图形，对称中心为（3，0），故①正确，②错；
在（-∞，+∞）递增，值域为（-6，6）
故③，函数 f（x）在[0，6]上是增函数，正确；
故④函数 f（x）没有最大值也没有最小值，正确；
故⑤无论m为何实数，关于x的方程 f（x）-m=0都有有实数根，错．
故答案为：①③④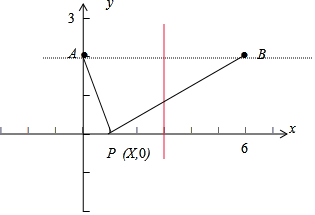

点评 本题考查了函数表达式的几何意义，属于中档题．