
| A. | $(\frac{1-ln2}{8},\frac{1-ln2}{6})∪(\frac{ln2-1}{6},\frac{ln2-1}{8})$ | B. | $(\frac{ln2-1}{6},\frac{ln2-1}{8})$ | ||
| C. | $(\frac{1-ln2}{8},\frac{1-ln2}{6})$ | D. | $(\frac{1-ln2}{8},\frac{ln2-1}{6})$ |
分析 确定函数为偶函数则其周期为T=2,函数在x∈[1,2]为减函数,作出函数的图象,得出当x<0时,要使符合题意则$m∈(\frac{ln2-1}{6},\frac{ln2-1}{8})$,根据偶函数的对称性,当x>0时,要使符合题意则$m∈(\frac{1-ln2}{8},\frac{1-ln2}{6})$.即可得出结论.
解答 解:因为函数f(2-x)=f(x)可得图象关于直线x=1对称,且函数为偶函数则其周期为T=2,
又因为$f'(x)=\frac{1}{x}-1=\frac{1-x}{x}$,当x∈[1,2]时有f'(x)≤0,则函数在x∈[1,2]为减函数,
作出其函数图象如图所示:
其中${k_{OA}}=\frac{ln2-1}{6},{k_{OB}}=\frac{ln2-1}{8}$,当x<0时,要使符合题意则$m∈(\frac{ln2-1}{6},\frac{ln2-1}{8})$
根据偶函数的对称性,当x>0时,要使符合题意则$m∈(\frac{1-ln2}{8},\frac{1-ln2}{6})$.
综上所述,实数m的取值范围为$(\frac{1-ln2}{8},\frac{1-ln2}{6})∪(\frac{ln2-1}{6},\frac{ln2-1}{8})$,
故选A.
点评 本题考查函数的奇偶性、单调性,考查数形结合的数学思想,难度大.


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:解答题
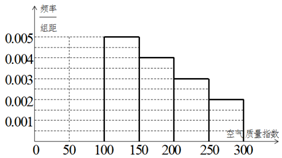 某中学环保社团参照国家环境标准,制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):
某中学环保社团参照国家环境标准,制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):| 空气质量指数 | (0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] |
| 空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
| 空气质量指数 | 频数 | 频率 |
| (0,50] | x | a |
| (50,100] | y | b |
| (100,150] | 25 | 0.25 |
| (150,200] | 20 | 0.2 |
| (200,250] | 15 | 0.15 |
| (250,300] | 10 | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | (0,1] | C. | (0,1) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若0<α<$\frac{π}{2}$,则sinα<tanα | |
| B. | 若α是第二象限角,则$\frac{α}{2}$为第一象限或第三象限角 | |
| C. | 若角α的终边过点P(3k,4k)(k≠0),则sinα=$\frac{4}{5}$ | |
| D. | 若扇形的周长为6,半径为2,则其中心角的大小为1弧度 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
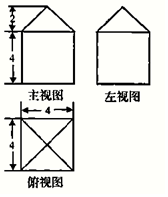
| A. | 96+16$\sqrt{2}$cm2 | B. | 80+16$\sqrt{2}$cm2 | C. | 96+32$\sqrt{2}$cm2 | D. | 80+32$\sqrt{2}$cm2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com