
分析 对4个选项分别进行判断,即可得出结论.
解答 解:①双曲线$\frac{x^2}{16}-\frac{y^2}{9}$=1的焦点坐标为(±5,0),椭圆$\frac{x^2}{49}+\frac{y^2}{24}$=1的焦点坐标为(±5,0),所以双曲线$\frac{x^2}{16}-\frac{y^2}{9}$=1与椭圆$\frac{x^2}{49}+\frac{y^2}{24}$=1有相同的焦点,正确;
②不妨设抛物线为标准抛物线:y2=2px (p>0 ),即抛物线位于Y轴的右侧,以X轴为对称轴.
设过焦点的弦为PQ,PQ的中点是M,M到准线的距离是d.
而P到准线的距离d1=|PF|,Q到准线的距离d2=|QF|.
又M到准线的距离d是梯形的中位线,故有d=$\frac{|PF|+|QF|}{2}$,
由抛物线的定义可得:$\frac{|PF|+|QF|}{2}$=$\frac{|PQ|}{2}$=半径.
所以圆心M到准线的距离等于半径,
所以圆与准线是相切,正确.
③平面内与两个定点F1,F2的距离的差的绝对值等于常数k(k<|F1F2|)的点的轨迹叫做双曲线,当0<k<|AB|时是双曲线的一支,当k=|AB|时,表示射线,所以不正确;
④设定圆C的方程为x2+y2+Dx+Ey+F=0,点A(m,n),P(x,y),由$\overrightarrow{OP}=\frac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB})$,可知P为AB的中点,则B(2x-m,2y-n),因为AB为圆的动弦,所以B在已知圆上,把B的坐标代入圆x2+y2+Dx+Ey+F=0得到P的轨迹仍为圆,当B与A重合时AB不是弦,所以点A除外,所以不正确.
故答案为:①②.
点评 本题主要考查了圆锥曲线的共同特征,同时考查了椭圆与双曲线的性质,考查的知识点较多,属于中档题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案科目:高中数学 来源: 题型:解答题
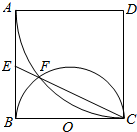 如图,正方形ABCD中,以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连接CF并延长交AB于点E.
如图,正方形ABCD中,以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连接CF并延长交AB于点E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
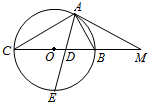 如图所示,MA为圆O的切线,A为切点,割线MC交圆O于B,C两点,MA=6,MB=3,AB=$\sqrt{17}$,∠BAC的角平分线与BC和圆O分别交于点D,E.
如图所示,MA为圆O的切线,A为切点,割线MC交圆O于B,C两点,MA=6,MB=3,AB=$\sqrt{17}$,∠BAC的角平分线与BC和圆O分别交于点D,E.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
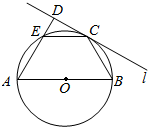 如图,AB是圆O的直径,C为圆周上一点,过C作圆O的切线l,过A作直线l的垂线AD,D为垂足,AD与圆O交于点E.
如图,AB是圆O的直径,C为圆周上一点,过C作圆O的切线l,过A作直线l的垂线AD,D为垂足,AD与圆O交于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com