
分析 (1)设M(x,y),$x≥\sqrt{2}$,左焦点${F_1}(-\sqrt{5},0)$,通过$\overrightarrow{OM}•\overrightarrow{{F_1}M}=(x,y)•(x+\sqrt{5},y)$利用二次函数的性质求出对称轴$x=-\frac{{\sqrt{5}}}{5}≤\sqrt{2}$,求出$\overrightarrow{OM}•\overrightarrow{{F_1}M}$的取值范围.
(2)写出P点轨迹为椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$,利用$|{{F_1}{F_2}}|=2\sqrt{5}$,|PF1|+|PF2|=2a,结合余弦定理,以及基本不等式求解椭圆方程即可.
解答 解:(1)设M(x,y),$x≥\sqrt{2}$,左焦点${F_1}(-\sqrt{5},0)$,$\overrightarrow{OM}•\overrightarrow{{F_1}M}=(x,y)•(x+\sqrt{5},y)$=${x^2}+\sqrt{5}x+{y^2}={x^2}+\sqrt{5}x+\frac{{3{x^2}}}{2}-3$…(4分)
=$\frac{5}{2}{x^2}+\sqrt{5}x-3$($x≥\sqrt{2}$)
对称轴$x=-\frac{{\sqrt{5}}}{5}≤\sqrt{2}$,
$\overrightarrow{OM}•\overrightarrow{{F_1}M}∈[{2+\sqrt{10},+∞})$…(3分)
(2)由椭圆定义得:P点轨迹为椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$,$|{{F_1}{F_2}}|=2\sqrt{5}$,|PF1|+|PF2|=2a$cos∠{F_1}P{F_2}=\frac{{{{|{P{F_1}}|}^2}+{{|{P{F_2}}|}^2}-20}}{{2|{P{F_1}}|•|{P{F_2}}|}}=\frac{{4{a^2}-2|{P{F_1}}|•|{P{F_2}}|-20}}{{2|{P{F_1}}|•|{P{F_2}}|}}$=$\frac{{4{a^2}-20}}{{2|{P{F_1}}|•|{P{F_2}}|}}-1$…(4分)
由基本不等式得$2a=|{P{F_1}}|+|{P{F_2}}|≥2\sqrt{|{P{F_1}}|•|{P{F_2}}|}$,
当且仅当|PF1|=|PF2|时等号成立$|{P{F_1}}|•|{P{F_2}}|≤{a^2}$$⇒cos∠{F_1}P{F_2}≥\frac{{4{a^2}-20}}{{2{a^2}}}-1=-\frac{1}{9}⇒{a^2}=9$,b2=4
所求动点P的轨迹方程为$\frac{x^2}{9}+\frac{y^2}{4}=1$…(3分)
点评 本题考查直线与椭圆的位置关系的应用,椭圆方程的求法,考查计算能力.


科目:高中数学 来源: 题型:选择题
| x | -2 | -1 | 0 | 1 | 2 |
| y | 5 | 2 | 2 | 1 |
| A. | 3 | B. | 4 | C. | 5 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{1}{2}})$ | B. | $({\frac{1}{2},1})$ | C. | (0,1) | D. | $({0,\frac{1}{2}})∪$$({\frac{1}{2},1})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12种 | B. | 13种 | C. | 14种 | D. | 15种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
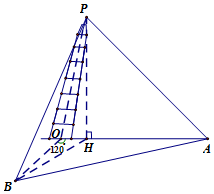 上海市松江区天马山上的“护珠塔”因其倾斜度超过意大利的比萨斜塔而号称“世界第一斜塔”.兴趣小组同学实施如下方案来测量塔的倾斜度和塔高:如图,记O点为塔基、P点为塔尖、点P在地面上的射影为点H.在塔身OP射影所在直线上选点A,使仰角k∠HAP=45°,过O点与OA成120°的地面上选B点,使仰角∠HPB=45°(点A、B、O都在同一水平面上),此时测得∠OAB=27°,A与B之间距离为33.6米.试求:
上海市松江区天马山上的“护珠塔”因其倾斜度超过意大利的比萨斜塔而号称“世界第一斜塔”.兴趣小组同学实施如下方案来测量塔的倾斜度和塔高:如图,记O点为塔基、P点为塔尖、点P在地面上的射影为点H.在塔身OP射影所在直线上选点A,使仰角k∠HAP=45°,过O点与OA成120°的地面上选B点,使仰角∠HPB=45°(点A、B、O都在同一水平面上),此时测得∠OAB=27°,A与B之间距离为33.6米.试求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com