
分析 (1)由题意可知:$\left\{\begin{array}{l}{sinx≥0}\\{\frac{1}{2}-cosx≥0}\end{array}\right.$,即可求得函数的定义域;
(2)利用同角三角函数的基本关系及二次函数的性质可知y=-(sinx+$\frac{1}{2}$)2+$\frac{5}{4}$,由x的取值范围,sinx∈[-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$],由二次函数的性质即可求得函数的值域.
解答 解:(1)由题意可知:$\left\{\begin{array}{l}{sinx≥0}\\{\frac{1}{2}-cosx≥0}\end{array}\right.$
解得:$\left\{\begin{array}{l}{2kπ≤x≤π+2kπ}\\{\frac{π}{3}+2kπ≤x≤\frac{5π}{3}+2kπ}\end{array}\right.$(k∈Z),
即2kπ+$\frac{π}{3}$≤x≤2kπ+π,(k∈Z),
∴函数的定义域为:{x丨2kπ+$\frac{π}{3}$≤x≤2kπ+π(k∈Z)};
(2)y=cos2x-sinx=-sin2x-sinx+1=-(sinx+$\frac{1}{2}$)2+$\frac{5}{4}$,
x∈[-$\frac{π}{4}$,$\frac{π}{4}}$],
∴sinx∈[-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$],
故当sinx=-$\frac{1}{2}$时,函数取得最大值为$\frac{5}{4}$,当sinx=$\frac{\sqrt{2}}{2}$时,函数取得最小值为$\frac{2-2\sqrt{2}}{4}$.
点评 本题考查函数的定义域及值域的求法,考查同角三角函数基本关系,正弦函数图象及性质,二次函数的性质,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
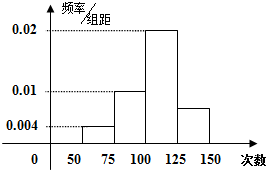 为了了解小学生的体能情况,抽取了某校一个年级的部分学生进行一分钟跳绳次数测试,将所得的数据整理后,画频率分布直方图.已知图中横轴从左向右的分组为[50,75)、[75,100)、[100,125)、[125,150],纵轴前3个对应值分别为0.004、0.01、0.02,因失误第4个对应值丢失.
为了了解小学生的体能情况,抽取了某校一个年级的部分学生进行一分钟跳绳次数测试,将所得的数据整理后,画频率分布直方图.已知图中横轴从左向右的分组为[50,75)、[75,100)、[100,125)、[125,150],纵轴前3个对应值分别为0.004、0.01、0.02,因失误第4个对应值丢失.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 6π+12 | B. | 6π+24 | C. | 12π+12 | D. | 24π+12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com