
����Ŀ��![]() ij��˾Ϊ�˽��û������Ʒ������ȣ���A,B�������ֱ����������20���û����õ��û��Բ�Ʒ�������ƽ�����£�
ij��˾Ϊ�˽��û������Ʒ������ȣ���A,B�������ֱ����������20���û����õ��û��Բ�Ʒ�������ƽ�����£�
A������62 73 81 92 95 85 74 64 53 76
78 86 95 66 97 78 88 82 76 89
B������73 83 62 51 91 46 53 73 64 82
93 48 65 81 74 56 54 76 65 79
��1����I������������������������û���������ֵľ�Ҷͼ����ͨ����Ҷͼ�Ƚ���������������ֵ�ƽ��ֵ����ɢ�̶ȣ���Ҫ����������ֵ���ó����ۼ��ɣ�
��2����II�������û���������֣����û�������ȴӵ͵��߷�Ϊ�����ȼ���
|
|
|
|
|
|
|
|
��ʱ��C����A�����û�������ȵȼ�����B�����û�������ȵȼ����������������û������۽��������������������ݣ����¼�������Ƶ����Ϊ��Ӧ�¼������ĸ��ʣ���C�ĸ��ʡ�
���𰸡�
��1��
�����������û���������ֵľ�Ҷͼ����
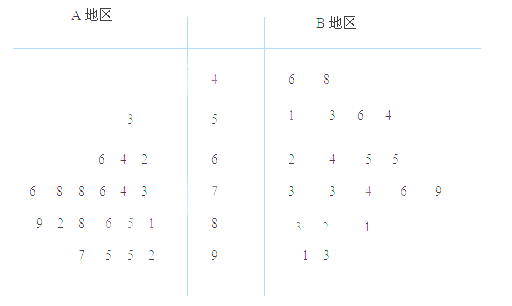
ͨ����Ҷͼ���Կ�����A�����û���������ֵ�ƽ��ֵ����B�����û���������ֵ�ƽ��ֵ��A�����û���������ֱȽϼ��У�B�����û���������ֱȽϷ�ɢ��
��2��
��P(C)=![]() x
x![]() +
+![]() x
x![]() =0.48
=0.48
����������II��
��CA1��ʾ�¼�����A�����û�����ȵȼ�Ϊ�����dz����⡱
CA2��ʾ�¼�����A�����û�����ȵȼ�Ϊ�dz����⡱
CB1��ʾ�¼�����B�����û�����ȵȼ�Ϊ�����⡱
CB2��ʾ�¼�����B�����û�����ȵȼ�Ϊ���⡱
��CA1��CB1������CA2��CB2������CB1��CB2���⣬C=CB1CA1![]() CB2CA2
CB2CA2
P(C)=P(CB1CA1![]() CB2CA2)=P(CB1CA1)+P(CB2CA2)=P(CB1)P(CA1)+P(CB2)P(CA2)
CB2CA2)=P(CB1CA1)+P(CB2CA2)=P(CB1)P(CA1)+P(CB2)P(CA2)
���������ݵ�CA1 �� CA2��CB1��CB2�����ĸ���Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ����P(CA1)=
����P(CA1)=![]() ,P(CA2)=
,P(CA2)=![]() ,P(CB1)=
,P(CB1)=![]() ,P(CB2)=
,P(CB2)=![]()
��P(C)=![]() x
x![]() +
+![]() x
x![]() =0.48
=0.48
�����㾫����������Ŀ����֪���������þ�Ҷͼ�ͻ����¼�������¼������֪ʶ���Եõ�����Ĵ𰸣���Ҫ���վ�Ҷͼ�ֳơ�֦Ҷͼ��������˼·�ǽ������е�����λ�����бȽϣ������Ĵ�С���������仯�����λ��Ϊһ�����ɣ����������仯���λ������Ϊ��֦��Ҷ�����������ɵĺ��棬�����Ϳ�������ؿ���ÿ�����ɺ���ļ�������ÿ���������Ƕ��٣������¼���ָ�¼�A���¼�B��һ�������в���ͬʱ�����������������ֲ�ͬ�����Σ���1���¼�A�������¼�B����������2���¼�A���������¼�B��������3���¼�A���¼�Bͬʱ���������������¼���ָ�¼�A���¼�B���ҽ���һ��������������������Σ���1���¼�A����B����������2���¼�B�����¼�A�������������¼������¼����������Σ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����P��˫���� ![]() ��a��0��b��0������֧�ϣ������ҽ���ֱ�ΪF1��F2 �� ֱ��PF1��������ԭ��OΪԲ�ġ�aΪ�뾶��Բ�����ڵ�A���߶�PF1�Ĵ�ֱƽ����ǡ�ù���F2 �� ���˫���ߵĽ����ߵ�б��Ϊ�� ��
��a��0��b��0������֧�ϣ������ҽ���ֱ�ΪF1��F2 �� ֱ��PF1��������ԭ��OΪԲ�ġ�aΪ�뾶��Բ�����ڵ�A���߶�PF1�Ĵ�ֱƽ����ǡ�ù���F2 �� ���˫���ߵĽ����ߵ�б��Ϊ�� ��
A.�� ![]()
B.�� ![]()
C.�� ![]()
D.�� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڼ�����ABCDEF�У��ı���ABCD�����Σ�BE��ƽ��ABCD��DF��BE����DF=2BE=2��EF=3�� 
��1��֤����ƽ��ACF��ƽ��BEFD
��2���������A��EF��C�Ƕ���ǣ���ֱ��AE��ƽ��ABCD���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() ij��˾Ϊ���˽��û������Ʒ�������,��A,B�������ֱ����������40���û�,���� �û������Ʒ������ȵ�����,�õ�A�����û���������ֵ�Ƶ�ʷֲ�ֱ��ͼ��B�����û���������ֵ�Ƶ�ʷֲ���.A�����û���������ֵ�Ƶ�ʷֲ�ֱ��ͼ
ij��˾Ϊ���˽��û������Ʒ�������,��A,B�������ֱ����������40���û�,���� �û������Ʒ������ȵ�����,�õ�A�����û���������ֵ�Ƶ�ʷֲ�ֱ��ͼ��B�����û���������ֵ�Ƶ�ʷֲ���.A�����û���������ֵ�Ƶ�ʷֲ�ֱ��ͼ
B�����û���������ֵ�Ƶ�ʷֲ���
��������ַ��� | [50��60) | [50��60) | [50,60) | [50,60) | [50,60) |
Ƶ�� | 2 | 8 | 14 | 10 | 6 |
��1����I���ڴ��������B�����û���������ֵ�Ƶ�ʷֲ�ֱ��ͼ,��ͨ����ͼ�Ƚ���������������ֵ�ƽ��ֵ���� ɢ �̶�.����Ҫ����������ֵ,�������ۼ��ɣ�
B�����û���������ֵ�Ƶ�ʷֲ�ֱ��ͼ
��2����II�������û����������,���û�����������ַ�Ϊ�����ȼ���
��������� | ����70�� | 70�ֵ�89�� | ������90�� |
����ȵȼ� | ������ | ���� | �dz����� |
�����Ǹ��������û�������ȵȼ�Ϊ������ĸ��ʴ�,˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() ��a��b��c��d��Ϊ��������a+b=c+d��֤������1����ab > cd����
��a��b��c��d��Ϊ��������a+b=c+d��֤������1����ab > cd���� ![]() +
+![]() >
>![]() +
+ ![]() ����2��
����2�� ![]() +
+![]() >
> ![]() +
+ ![]() ��|a-b| < |c-d|�ij�Ҫ����
��|a-b| < |c-d|�ij�Ҫ����
��1����I����ab![]() cd����
cd����![]() +
+![]()
![]()
![]() +
+![]()
��2��(II)![]() +
+![]()
![]()
![]() +
+![]() ��|a-b|
��|a-b|![]() |c-d|�ij�Ҫ����
|c-d|�ij�Ҫ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(2015![]() �¿α�II)��ֱ������ϵxoy�У�����C1��
�¿α�II)��ֱ������ϵxoy�У�����C1��![]() (tΪ������t��0)������0
(t������t��0)������0![]()
![]()
![]() ������OΪ���㣬x��������Ϊ����ļ�����ϵ�У�����C2��
������OΪ���㣬x��������Ϊ����ļ�����ϵ�У�����C2��![]() =2sin
=2sin![]() ��C3:
��C3:![]() =2
=2![]() cos
cos![]()
��1��������C2��C1�����ֱ������
��2��������C2��C1�ཻ�ڵ�A��C3��C1�ཻ�ڵ�B����|AB|�����ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(2015���¿α�I����ij��˾Ϊȷ����һ���Ͷ��ij�ֲ�Ʒ�������ѣ����˽���������x����λ��ǧԪ������������y����λ��t����������z����λ��ǧԪ����Ӱ�죬�Խ�8���������xi����������yi=1;2��8�������˳����������õ������ɢ��ͼ��һЩͳ������ֵ.
|
|
|
|
|
|
|
46.6 | 56.3 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
����wi=![]() ��
��![]() =
=![]()
��1������ɢ��ͼ�жϣ�y=a+bx��y=c+d![]() ����һ��������Ϊ��������y������������x�Ļع鷽�����ͣ������жϼ��ɣ�����˵�����ɣ���
����һ��������Ϊ��������y������������x�Ļع鷽�����ͣ������жϼ��ɣ�����˵�����ɣ���
��2�����ݣ�I�����жϽ�����������ݣ�����y����x�Ļع鷽�̣�
��3����֪���ֲ�Ʒ��������z��x �� y�Ĺ�ϵΪz=0.2y-x�����ݣ�II���Ľ���ش��������⣺
��i������������x=90ʱ�������������������Ԥ��ֵʱ���٣�
��ii������������xΪ��ֵʱ���������Ԥ��ֵ���
��������һ������(u1,v1),(u2,v2)��������(un,vn),��ع���v=![]() ��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ��
��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(2015���Ĵ���������{an}��ǰn���Sn=2an-a1 �� ��a1, a2+1, a3�ɵȲ�����.
��1��������{an}��ͨ�ʽ��
��2��������{![]() }��ǰn���Tn �� ��Tn��
}��ǰn���Tn �� ��Tn��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(2015�����ϣ����ABC���ڽ�A��B��C�ĶԱ߷ֱ�Ϊa��b��c��a=btanA��
��1��֤����sinB=cosA
��2����sinC-sinAcosB=![]() ,��BΪ�۽ǣ���A,B,C
,��BΪ�۽ǣ���A,B,C
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com