设函数
，
．
（1）当
时，求函数
的单调区间及所有零点；
（2）设
，
，
为函数
图象上的三个不同点，且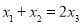
，问：是否存在实数
，使得函数
在点
处的切线与直线
平行？若存在，求出所有满足条件的实数
的值；若不存在，请说明理由．
科目：高中数学 来源：2017届河南南阳一中高三文上学期月考四数学试卷（解析版） 题型：解答题
选修4-4：极坐标与参数方程
在平面直角坐标系
中，曲线
的参数方程为
（
为参数）．
（1）求曲线
的普通方程；
（2）经过点
（平面直角坐标系
中点）作直线
交曲线
于
，
两点，若
恰好为线段
的三等分点，求直线
的斜率．
查看答案和解析>>
科目：高中数学 来源：2017届贵州遵义南白中学高三文上学期联考四数学试卷（解析版） 题型：选择题
已知在三棱锥
中，
，
，
，平面
平面
，若三棱锥的顶点在同一个球面上，则该球的表面积为（ ）
A．
B．
C．
D．
查看答案和解析>>
科目：高中数学 来源：2017届贵州遵义南白中学高三文上学期联考四数学试卷（解析版） 题型：选择题
甲、乙两棉农，统计连续五年的面积产量（千克/亩）如下表：
棉农甲 | 68 | 72 | 70 | 69 | 71 |
棉农乙 | 69 | 71 | 68 | 68 | 69 |
则平均产量较高与产量较稳定的分别是（ ）
A．棉农甲，棉农甲 B．棉农甲，棉农乙
C．棉农乙，棉农甲 D．棉农乙，棉农乙
查看答案和解析>>
科目：高中数学 来源：2017届贵州遵义南白中学高三理上学期联考四数学试卷（解析版） 题型：选择题
下列四个命题正确的是（ ）
①设集合
，
，则“
”是“
”的充分不必要条件；
②命题“若
，则
”的逆否命题是“若
，则
”；
③若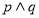
是假命题，则
，
都是假命题；
④命题
：“
，
”的否定为
：“
，
”．
A．①②③④ B．①③④ C．②④ D．②③④
查看答案和解析>>
科目：高中数学 来源：2017届湖南长沙一中高三文月考五数学试卷（解析版） 题型：解答题
如图，在梯形
中，
，
，
，
、
分别是
、
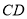上的点，
，
，沿将梯形翻折，使平面
平面
，
是
的中点.
（1）当
时，求证：
；
（2）当
变化时，求三棱锥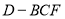
的体积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
是
上的偶函数，设
，
，
，当任意
，
时，都有
，则（ ）
B．
D．
是等比数列，公比
，
为
的前
项和，记
，
，设
设为数列
的最大项，则
．
，
满足
则
的最大值是 ．