Question

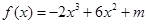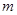已知（为常数）在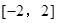上有最小值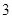，那么此函数在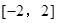上的最大值为(       )

A．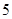

B．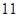

C．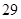

D．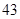

Answer 1

D  

解析试题分析：由已知，f′（x）=－6x²+12x，由－6x²+12x≥0得0≤x≤2，
因此当x∈[2，+∞），（－∞，0]时f（x）为减函数，在x∈[0，2]时f（x）为增函数，
又因为x∈[-2，2]，所以得
当x∈[－2，0]时f（x）为减函数，在x∈[0，2]时f（x）为增函数，
所以f（x）_min=f（0）=m=3，故有f（x）=－2x³＋6x²+3
所以f（－2）=43，f（2）=11，,函数f（x）的最小值为f（－2）=43．故选D。
考点：本题主要考查应用导数研究函数的单调性，最值。
点评：小综合题，在某区间，导函数值非负，则函数为增函数；导函数值非正，则函数为减函数。确定最值，可遵循“求导数，求驻点，计算驻点及区间端点函数值，比较确定最值”。