
分析 (Ⅰ)利用已知条件直接计算a1,a2,a3,a4的值;
(Ⅱ)猜想an的表达式,用数学归纳法证明步骤,逐步证明猜想成立即可.
解答 解:(Ⅰ)计算得:a1=1,a2=$\frac{3}{2}$,a3=$\frac{7}{4}$,a4=$\frac{15}{8}$,…(4分)
(Ⅱ)猜想an=$\frac{{2}^{n}-1}{{2}^{n-1}}$.…(6分)
证明:?当n=1时,计算的a1=1=$\frac{{2}^{1}-1}{{2}^{1-1}}$,猜想成立; …(7分)
?假设当n=k(k≥1)时猜想成立,即ak=$\frac{{2}^{k}-1}{{2}^{k-1}}$,…(8分)
则当n=k+1时,Sk=2k-ak,Sk+1=2(k+1)-ak+1,
所以ak+1=Sk+1-Sk=2(k+1)-ak+1-2k+ak,
=2+ak-ak+1所以ak+1=1+$\frac{{a}_{k}}{2}$=1+$\frac{{2}^{k}-1}{{2}^{k}}$=$\frac{{2}^{k+1}-1}{{2}^{k+1-1}}$,
所以当当n=k+1时,猜想也成立.…(11分)
综合??可知:猜想an=$\frac{{2}^{n}-1}{{2}^{n-1}}$,n∈N*,成立.…(12分)
点评 本题考查数学归纳法的应用,考查逻辑推理能力以及计算能力.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | (-∞,-1]∪[1,+∞) | C. | (-1,1] | D. | (-∞,-1)∪[1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
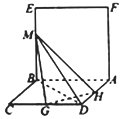 如图,已知平面ABEF⊥平面ABCD,四边形ABEF是正方形,四边形ABCD是菱形,且BC=2,∠BAD=60°,点G,H分别为边CD,DA的中点,点M是线段BE上的动点.
如图,已知平面ABEF⊥平面ABCD,四边形ABEF是正方形,四边形ABCD是菱形,且BC=2,∠BAD=60°,点G,H分别为边CD,DA的中点,点M是线段BE上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (9,10) | B. | (1,9) | C. | (0,9) | D. | (9,11) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com