
已知函数 .
.
(1)求函数 的单调递增区间;
的单调递增区间;
(2)若 是
是 的三个内角,且
的三个内角,且 ,
, ,又
,又 ,求
,求 边的长.
边的长.
(1)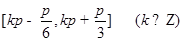 ;(2)
;(2)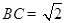 或
或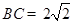 .
.
解析试题分析:本题考查三角恒等变换、三角函数图象及其性质、解三角形等基础知识;考查学生运算求解能力;考查数形结合思想和分类整合思想.第一问,利用两角差的正弦公式、倍角公式化简表达式,使之化简为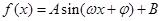 的形式,再结合
的形式,再结合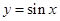 图象求函数的单调递增区间;第二问,利用第一问化简的表达式,由
图象求函数的单调递增区间;第二问,利用第一问化简的表达式,由 ,先求出A角的值,由于A角得到2个值,所以分情况讨论,利用正弦定理求BC的长.
,先求出A角的值,由于A角得到2个值,所以分情况讨论,利用正弦定理求BC的长.
试题解析:(1)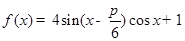
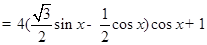 1分
1分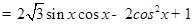
 3分
3分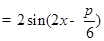 4分
4分
令  5分
5分
解得 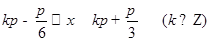
∴函数 的递增区间是
的递增区间是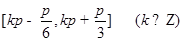 . 6分
. 6分
(2)由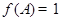 得,
得, 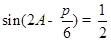 ,∵
,∵ , ∴
, ∴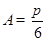 或
或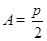 . 8分
. 8分
(1)当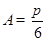 时,由正弦定理得,
时,由正弦定理得,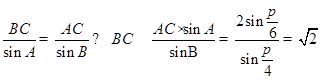 ; 10分
; 10分
(2) 当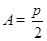 时,由正弦定理得,
时,由正弦定理得, . 12分
. 12分
综上,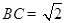 或
或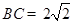 . 13分
. 13分
考点:三角恒等变换、三角函数图象及其性质、解三角形.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分)定义在区间 上的函数
上的函数 的图象关于直线
的图象关于直线 对称,当
对称,当 时函数
时函数 图象如图所示.
图象如图所示.
(1)求函数 在
在 的表达式;
的表达式;
(2)求方程 的解;
的解;
(3)是否存在常数 的值,使得
的值,使得 在
在 上恒成立;若存在,求出
上恒成立;若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,某市新体育公园的中心广场平面图如图所示,在y轴左侧的观光道曲线段是函数 ,
, 时的图象且最高点B(-1,4),在y轴右侧的曲线段是以CO为直径的半圆弧.⑴试确定A,
时的图象且最高点B(-1,4),在y轴右侧的曲线段是以CO为直径的半圆弧.⑴试确定A, 和
和 的值;⑵现要在右侧的半圆中修建一条步行道CDO(单位:米),在点C与半圆弧上的一点D之间设计为直线段(造价为2万元/米),从D到点O之间设计为沿半圆弧的弧形(造价为1万元/米).设
的值;⑵现要在右侧的半圆中修建一条步行道CDO(单位:米),在点C与半圆弧上的一点D之间设计为直线段(造价为2万元/米),从D到点O之间设计为沿半圆弧的弧形(造价为1万元/米).设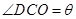 (弧度),试用
(弧度),试用 来表示修建步行道的造价预算,并求造价预算的最大值?(注:只考虑步行道的长度,不考虑步行道的宽度)
来表示修建步行道的造价预算,并求造价预算的最大值?(注:只考虑步行道的长度,不考虑步行道的宽度)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com