
分析 (Ⅰ)函数的定义域为(0,+∞),$f′(x)=\frac{{e}^{x}(x-1)}{{x}^{2}}-\frac{m}{x}+\frac{m}{{x}^{2}}$=$\frac{(x-1)({e}^{x}-m)}{{x}^{2}}$.令f′(x)=0,可得x=1,或x=lnm
分①m=e,②m>e,③1<m<e分类讨论其单调性;
(Ⅱ)g(x)=x2f′(x)-xex=-ex-m(x-1)在($\frac{3}{2}$,3)内有两个零点,
?方程-ex-m(x-1)=0在($\frac{3}{2}$,3)内有两个实根,
即m=-$\frac{{e}^{x}}{x-1}$在($\frac{3}{2}$,3)内有两个实根,
令h(x)=-$\frac{{e}^{x}}{x-1}$,可得h(x)在($\frac{3}{2},2$)递增,在(2,3),递减,
要使g(x)=x2f′(x)-xex在($\frac{3}{2}$,3)内有两个零点,则$\left\{\begin{array}{l}{m>h(\frac{3}{2})=-2{e}^{\frac{3}{2}}}\\{m>h(3)=-\frac{1}{2}{e}^{3}}\\{m<h(2)=-{e}^{2}}\end{array}\right.$
可得实数m的取值范围为(-$\frac{1}{2}{e}^{3}$,-e2).
(Ⅲ)当m=1时,要证xf(x)+xlnx+1>x+$\frac{ln(x+1)}{x}$.只证x($\frac{{e}^{x}}{x}$-lnx-$\frac{1}{x}$)+xlnx+1>x+$\frac{ln(x+1)}{x}$在(0,+∞)恒成立.
只证${e}^{x}>x+\frac{ln(x+1)}{x}$,易得ex>x+1在(0,+∞)恒成立,
故只需证1>$\frac{ln(x+1)}{x}$,即证x>ln(x+1)即可,
解答 解:(Ⅰ)函数的定义域为(0,+∞),$f′(x)=\frac{{e}^{x}(x-1)}{{x}^{2}}-\frac{m}{x}+\frac{m}{{x}^{2}}$=$\frac{(x-1)({e}^{x}-m)}{{x}^{2}}$.
∵m>1,令f′(x)=0,可得x=1,或x=lnm
①当m=e时,f′(x)≥0在(0,+∞)恒成立,∴此时f(x)在(0,+∞)递增;
②当m>e时,x∈(0,1)时,f′(x)>0,x∈(1,lnm)时,f′(x)<0,x∈(lnm,+∞)时,f′(x)>0
此时f(x)在(lnm,+∞),(0,1)递增,在(1,lnm)递减.
③当1<m<e时,x∈(0,lnm)时,f′(x)>0,x∈(lnm,1)时,f′(x)<0,x∈(1,+∞)时,f′(x)>0
此时f(x)在(1,+∞),(0,lnm)递增,在(lnm,1)递减.
(Ⅱ)g(x)=x2f′(x)-xex=-ex-m(x-1)在($\frac{3}{2}$,3)内有两个零点,
?方程-ex-m(x-1)=0在($\frac{3}{2}$,3)内有两个实根,
即m=-$\frac{{e}^{x}}{x-1}$在($\frac{3}{2}$,3)内有两个实根,
令h(x)=-$\frac{{e}^{x}}{x-1}$,h′(x)=$\frac{{e}^{x}(2-x)}{(1-x)^{2}}$=0,可得x=2,
x$∈(\frac{3}{2},2)$时,h′(x)>0,x∈(2,3)时,h′(x)<0,
∴h(x)在($\frac{3}{2},2$)递增,在(2,3),递减,
要使g(x)=x2f′(x)-xex在($\frac{3}{2}$,3)内有两个零点,则$\left\{\begin{array}{l}{m>h(\frac{3}{2})=-2{e}^{\frac{3}{2}}}\\{m>h(3)=-\frac{1}{2}{e}^{3}}\\{m<h(2)=-{e}^{2}}\end{array}\right.$
可得-$\frac{1}{2}{e}^{3}$<m<-e2,∴实数m的取值范围为(-$\frac{1}{2}{e}^{3}$,-e2).
(Ⅲ)证明:当m=1时,要证xf(x)+xlnx+1>x+$\frac{ln(x+1)}{x}$.
只证x($\frac{{e}^{x}}{x}$-lnx-$\frac{1}{x}$)+xlnx+1>x+$\frac{ln(x+1)}{x}$在(0,+∞)恒成立.
只证${e}^{x}>x+\frac{ln(x+1)}{x}$,易得ex>x+1在(0,+∞)恒成立,
故只需证1>$\frac{ln(x+1)}{x}$,即证x>ln(x+1),
令F(x)=x-ln(x+1),F′(x)=1-$\frac{1}{x+1}$>0,故F(x)在(0,+∞)递增,而F(0)=0
∵F(x)>0在(0,+∞)恒成立.
∴xf(x)+xlnx+1>x+$\frac{ln(x+1)}{x}$成立.
点评 本题考查了导数的综合应用,考查了分类讨论思想、函数与方程思想,放缩法证明函数恒等式,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | $a>\frac{1}{2}$ | B. | a>$\frac{1}{3}$ | C. | 0<a<$\frac{1}{2}$ | D. | a>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
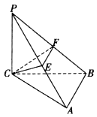 如图,已知在三棱锥P-ABC中,PC⊥平面ABC,AB⊥BC,若PC=BC=8,AB=4,E,F分别是PA,PB的中点,设三棱锥P-CEF的外接球的球心为O,则△AOB的面积为8$\sqrt{5}$.
如图,已知在三棱锥P-ABC中,PC⊥平面ABC,AB⊥BC,若PC=BC=8,AB=4,E,F分别是PA,PB的中点,设三棱锥P-CEF的外接球的球心为O,则△AOB的面积为8$\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{20}$ | B. | $\frac{1}{50}$ | C. | $\frac{1}{100}$ | D. | $\frac{1}{200}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com