【题目】在
中，三个内角
所对的边分别为
，满足
.
（1） 求角
的大小；
（2） 若
，求
，
的值.（其中
）
【答案】（1）
；（2）4，6
【解析】
（1）已知等式利用正弦定理化简，整理后利用两角和与差的正弦函数公式及诱导公式化简，求出
的值，即可确定出
的度数；（2）根据平面向量数量积的运算法则计算得到一个等式
，记作①，把的度数代入求出
的值,记作②,然后利用余弦定理表示出
，把
及的值代入求出
的值，利用完全平方公式表示出
，把相应的值代入，开方求出
的值,由②③可知
与
为一个一元二次方程的两个解,求出方程的解,根据大于，可得出，的值.
（1）已知等式
，
利用正弦定理化简得
，
整理得
，
即
，
，
则
.
（2）由
，得
， ①
又由（1）
，②
由余弦定理得
，
将
及①代入得
，
，
，③
由②③可知与为一个一元二次方程
的两个根，
解此方程，并由大于，可得
.
科目：高中数学 来源： 题型：
【题目】为了解学生的课外阅读时间情况，某学校随机抽取了 50人进行统计分析，把这50人每天阅读的时间(单位:分钟)绘制成频数分布表，如下表所示：
若把每天阅读时间在60分钟以上（含60分钟）的同学称为“阅读达人”，根据统计结果中男女生阅读达人的数据，制作出如图所示的等高条形图.
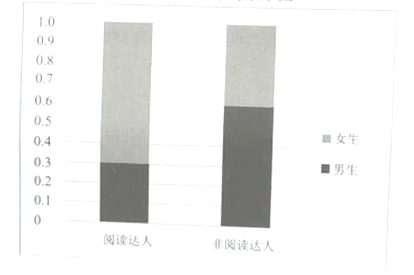
（1）根据抽样结果估计该校学生的每天平均阅读时间（同一组数据用该区间的中点值作为代表）；
（2）根据已知条件完成下面的
列联表，并判断是否有
的把握认为“阅读达人”跟性别有关？
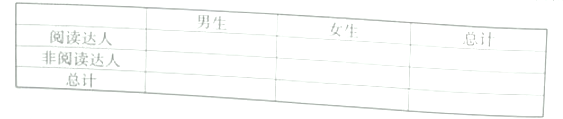
附：参考公式
，其中
.
临界值表：
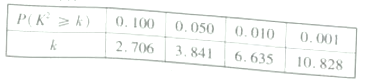
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设E，F分别是正方体ABCD﹣A1B1C1D1的棱DC上两点，且AB＝2，EF＝1，给出下列四个命题：
①三棱锥D1﹣B1EF的体积为定值；
②异面直线D1B1与EF所成的角为45°；
③D1B1⊥平面B1EF；
④直线D1B1与平面B1EF所成的角为60°．
其中正确的命题为_____．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=﹣alnx+（a+1）x﹣
（a＞0）．
（1）讨论函数f（x）的单调性；
（2）若f（x）≥﹣+ax+b恒成立，求a
时，实数b的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知菱形
，
在
轴上且
，
（
，
）．
（Ⅰ）求
点轨迹
的方程；
（Ⅱ）延长
交轨迹于点
，轨迹在点处的切线与直线
交于点
，试判断以为圆心，线段
为半径的圆与直线的位置关系，并证明你的结论．
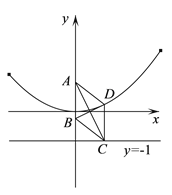
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为保护农民种粮收益，促进粮食生产，确保国家粮食安全，调动广大农民粮食生产的积极性，从2004年开始，国家实施了对种粮农民直接补贴.通过对2014～2018年的数据进行调查，发现某地区发放粮食补贴额
（亿元）与该地区粮食产量
（万亿吨）之间存在着线性相关关系.统计数据如下表：
年份 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 |
补贴额 | 9 | 10 | 12 | 11 | 8 |
粮食产量 | 23 | 25 | 30 | 26 | 21 |
（1）请根据如表所给的数据，求出关于的线性回归直线方程
；
（2）通过对该地区粮食产量的分析研究，计划2019年在该地区发放粮食补贴额7亿元，请根据（1）中所得的线性回归直线方程，预测2019年该地区的粮食产量.
（参考公式：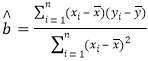
，
）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知等腰梯形ABCD(如图1所示)，其中AB∥CD，E，F分别为AB和CD的中点，且AB＝EF＝2，CD＝6，M为BC中点．现将梯形ABCD沿着EF所在直线折起，使平面EFCB⊥平面EFDA(如图2所示)，N是线段CD上一动点，且
.
(1)求证：MN∥平面EFDA；
(2)求三棱锥A－MNF的体积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
