
分析 (1)求出f(1)及f′(1)的值,代入点斜式方程即可得到答案;
(2)确定函数的定义域,求导函数.利用导数的正负,分类讨论,即可求得和的单调区间.
解答 解:函数y=f(x)的定义域为x∈(0,+∞),$f'(x)=2ax+\frac{1}{x}$
(1)可见,切点为P(1,1),切线的斜率k=f'(1)=3,
∴切线方程为y-1=3(x-1),即:3x-y-2=0;
(2)由题知:$f'(x)=2ax+\frac{1}{x}≥0$在(0,e]上恒成立,
∴$a≥-\frac{1}{{2{x^2}}}$在(0,e]上恒成立,
而x∈(0,e]时,$-\frac{1}{{2{x^2}}}≤-\frac{1}{{2{e^2}}}$,
∴$a≥-\frac{1}{{2{e^2}}}$.
点评 本题考查导数的几何意义,考查函数的单调区间,考查分类讨论的数学思想,考查学生分析解决问题的能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{10}$个单位长度 | B. | 向右平移$\frac{π}{10}$个单位长度 | ||
| C. | 向左平移$\frac{π}{5}$个单位长度 | D. | 向右平移$\frac{π}{5}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -4 | C. | $-\frac{1}{4}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
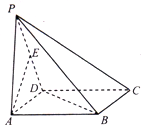 在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AB=AP,E为棱PD的中点
在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AB=AP,E为棱PD的中点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com