
分析 根据定积分求出a的值,再利用二项式展开式的通项公式求出展开式中的常数项.
解答 解:a=$\frac{2}{π}\int_{-1}^1{(\sqrt{1-{x^2}}+sinx)dx}$
=$\frac{2}{π}$${∫}_{-1}^{1}$$\sqrt{1{-x}^{2}}$dx+$\frac{2}{π}$${∫}_{-1}^{1}$sinxdx
=$\frac{2}{π}$×$\frac{1}{2}$arcsinx${|}_{-1}^{1}$-$\frac{2}{π}$cosx${|}_{-1}^{1}$
=$\frac{2}{π}$×$\frac{1}{2}$×π
=1,
∴二项式${(x-\frac{a}{x^2})^9}$=${(x-\frac{1}{{x}^{2}})}^{9}$,
其展开式通项公式为:
Tr+1=${C}_{9}^{r}$•x9-r•${(-\frac{1}{{x}^{2}})}^{r}$
=(-1)r•${C}_{9}^{r}$•x9-3r,
令9-3r=0,解得r=3,
∴展开式中的常数项为
T4=(-1)3•${C}_{9}^{3}$=-84.
故答案为:-84.
点评 本题考查了定积分与二项式展开式的通项公式应用问题,是综合题.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
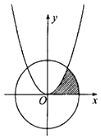 (x2+$\frac{a}{2x}$)6展开式的常数项是15,如图阴影部分是由曲线y=x2和圆x2+y2=a及x轴围成的封闭图形,则封闭图形面积为$\frac{π}{4}$-$\frac{1}{6}$.
(x2+$\frac{a}{2x}$)6展开式的常数项是15,如图阴影部分是由曲线y=x2和圆x2+y2=a及x轴围成的封闭图形,则封闭图形面积为$\frac{π}{4}$-$\frac{1}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3x-y-8=0 | B. | 3x+y+4=0 | C. | 3x-y+6=0 | D. | 3x+y+2=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图是一“T”型水渠的平面视图(俯视图),水渠的南北方向和东西方向轴截面均为矩形,南北向渠宽为4m,东西向渠宽$\sqrt{2}m$(从拐角处,即图中A,B处开始).假定渠内的水面始终保持水平位置(即无高度差).
如图是一“T”型水渠的平面视图(俯视图),水渠的南北方向和东西方向轴截面均为矩形,南北向渠宽为4m,东西向渠宽$\sqrt{2}m$(从拐角处,即图中A,B处开始).假定渠内的水面始终保持水平位置(即无高度差).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com