
| 1 | ||
2
|
| a1 |
| 2 |
| a2 |
| 22 |
| a3 |
| 23 |
| a2014 |
| 22014 |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| 1 |
| 2 |
| a1 |
| 2 |
| a2 |
| 22 |
| a3 |
| 23 |
| a2014 |
| 22014 |
| a1 |
| 2 |
| a2 |
| 22 |
| a3 |
| 23 |
| a2014 |
| 22014 |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| n(n-1) |
| 2 |
| 1 | ||
2
|
| C | r 10 |
| 5r |
| 2 |
| 5r |
| 2 |
| C | 8 10 |
| 45 |
| 256 |
| 1 |
| 2 |
| a1 |
| 2 |
| a2 |
| 22 |
| a3 |
| 23 |
| a2014 |
| 22014 |
| a1 |
| 2 |
| a2 |
| 22 |
| a3 |
| 23 |
| a2014 |
| 22014 |


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
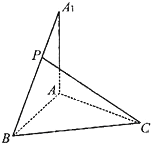 已知AA1⊥平面ABC,AA1=AB=BC=CA=3,P为A1B上的点.
已知AA1⊥平面ABC,AA1=AB=BC=CA=3,P为A1B上的点.| A1P |
| PB |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
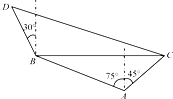 在海岸A处,发现北偏西75°的方向,与A距离2海里的B处有一艘走私船,在A处北偏东45°方向,与A距离(
在海岸A处,发现北偏西75°的方向,与A距离2海里的B处有一艘走私船,在A处北偏东45°方向,与A距离(| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小三角形构成,小三角形数越多刺绣越漂亮,现按同样的规律刺绣(小三角形的摆放规律相同),设第n个图形包含f(n)个小三角形.由图形知f(1)=1,f(2)=3,f(3)=6
某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小三角形构成,小三角形数越多刺绣越漂亮,现按同样的规律刺绣(小三角形的摆放规律相同),设第n个图形包含f(n)个小三角形.由图形知f(1)=1,f(2)=3,f(3)=6查看答案和解析>>
科目:高中数学 来源: 题型:
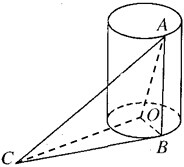 如图,AB是底面半径为1的圆柱的一条母线,O为下底面中心,BC是下底面的一条切线.
如图,AB是底面半径为1的圆柱的一条母线,O为下底面中心,BC是下底面的一条切线.查看答案和解析>>
科目:高中数学 来源: 题型:
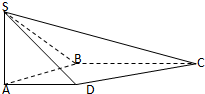 如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=1,BC=
如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=1,BC=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com