Question

5．设函数f（x）=（2x-1）e^x-ax+a，若存在唯一的整数x₀使得f（x₀）＜0，则实数a的取值范围是[$\frac{3}{2e}$，1）．

Answer 1

分析 首先令g（x）=（2x-1）e^x，h（x）=a（x-1），判断g（x）的单调性．因为存在唯一的整数x₀使得f（x₀）＜0．即（2x₀-1）e^x＜a（x₀-1）．所以结合图形知：$\left\{\begin{array}{l}{a＞0}\\{g（-1）≥h（-1）}\\{-1＜h（0）＜0}\end{array}\right.$

解答 解：令g（x）=（2x-1）e^x，h（x）=a（x-1），
∵g'（x）=（2x-1）e^x+2e^x=（2x+1）e^x，
∴当x＜-$\frac{1}{2}$时，g'（x）＜0，则函数g（x）在（-∞，-$\frac{1}{2}$）上单调递减；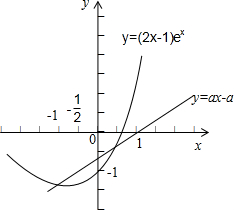
当x＞-$\frac{1}{2}$时，g'（x）＞0，则函数g（x）在（-$\frac{1}{2}$，+∞）上单调递增；
而g（-1）=-3e^-1，g（0）=-1；
因为存在唯一的整数x₀使得f（x₀）＜0．
即（2x₀-1）e^x＜a（x₀-1）．
所以结合图形知：$\left\{\begin{array}{l}{a＞0}\\{g（-1）≥h（-1）}\\{-1＜h（0）＜0}\end{array}\right.$ 或$\left\{\begin{array}{l}{h（2）＞g（2）}\\{h（3）＜g（3）}\end{array}\right.$
即：$\left\{\begin{array}{l}{a＞0}\\{-3{e}^{-1}≥-2a}\\{-1＜-a＜0}\end{array}\right.$或$\left\{\begin{array}{l}{a＞3{e}^{2}}\\{2a＜5{e}^{3}}\end{array}\right.$  解得$\frac{3}{2e}$≤a＜1或3e²＜a＜$\frac{5}{2}{e}^{3}$；
故答案为：[$\frac{3}{2e}$，1）∪$（3{e}^{2}，\frac{5}{2}{e}^{3}）$．

点评 本题主要考查了利用导数求函数的单调性，同时考查了函数与方程思想、转化思想，属中等题．