
在 中,
中,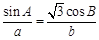 .
.
(1)求角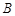 的值;
的值;
(2)如果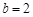 ,求
,求 面积的最大值.
面积的最大值.
科目:高中数学 来源: 题型:解答题
已知a、b、c分别是△ABC三个内角A、B、C的对边.
(1)若△ABC面积为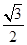 ,c=2,A=60º,求a,b的值;
,c=2,A=60º,求a,b的值;
(2)若acosA=bcosB,试判断△ABC的形状,证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
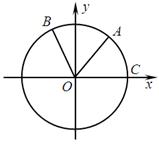
如图,点A、B是单位圆 上的两点,点C是圆
上的两点,点C是圆 与
与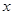 轴的正半轴的交点,将锐角
轴的正半轴的交点,将锐角 的终边
的终边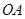 按逆时针方向旋转
按逆时针方向旋转 到
到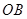 .
.
(1)若点A的坐标为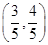 ,求
,求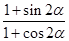 的值;
的值;
(2)用 表示
表示 ,并求
,并求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,某旅游景点有一座风景秀丽的山峰,山上有一条笔直的山路BC和一条索道AC,小王和小李打算不坐索道,而是花2个小时的时间进行徒步攀登.已知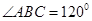 ,
,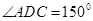 ,
,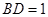 (千米),
(千米),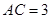 (千米).假设小王和小李徒步攀登的速度为每小时1200米,请问:两位登山爱好者能否在2个小时内徒步登上山峰.
(千米).假设小王和小李徒步攀登的速度为每小时1200米,请问:两位登山爱好者能否在2个小时内徒步登上山峰.
(即从B点出发到达C点)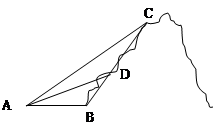
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com