
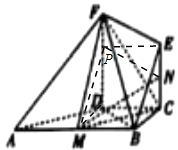
【题目】如图,在直角梯形ABCD中,AB∥CD,∠BCD=90°,BC=CD=2,AB=4,EC∥FD,FD⊥底面ABCD,M是AB的中点.
(1)求证:平面CFM⊥平面BDF;
(2)若点N为线段CE的中点,EC=2,FD=3,求证:MN∥平面BEF.
【答案】
(1)
证明:直角梯形ABCD中,AB∥CD,BC=2,AB=4,且M是AB的中点,
∴BM=CD,∴四边形BCDM是平行四边形,
又BC=CD=2,∴平行四边形BCDM是菱形;
∴BD⊥CM,
又FD⊥底面ABCD,CM平面BCDM,∴FD⊥CM,
且FD∩BD=D,
∴CM⊥平面BDF,
有CM平面CFM,
∴平面CFM⊥平面BDF;
(2)
过点N作NP∥EF,交DF与点P,连接PM,如图所示;
∵EC∥FD,∴四边形EFPN是平行四边形,
又点N为线段CE的中点,EC=2,FD=3,
∴FP= ![]() EC=1,
EC=1,
PD=EC=2,
∴PE∥CD,且PE=CD,
又BM∥CD,且BM=CD,
∴BM∥PE,且PE=BM,
∴四边形BEPM为平行四边形,
∴PM∥BE;
又PM平面BEF,BE平面BEF,∴PM∥平面BEF;
同理,PM∥平面BEF,
又PM∩PN=P,PM平面PMN,PN平面PMN,
∴平面PMN∥平面BEF,
又MN平面PMN,∴MN∥平面BEF.
【解析】(1)证明四边形BCDM是菱形,对角线BD⊥CM,再证明FD⊥CM,即可证明CM⊥平面BDF,从而得平面CFM⊥平面BDF;(2)过点N作NP∥EF,交DF与点P,连接PM,证明平面PMN∥平面BEF,即可证明MN∥平面BEF.
【考点精析】认真审题,首先需要了解直线与平面平行的判定(平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行),还要掌握平面与平面垂直的判定(一个平面过另一个平面的垂线,则这两个平面垂直)的相关知识才是答题的关键.


科目:高中数学 来源: 题型:
【题目】本着健康、低碳的生活理念,租自行车骑游的人越来越多.某自行车租车点的收费标准是每年每次租时间不超过两小时免费,超过两个小时的部分每小时收费2元(不足1小时的部分按1小时计算).现有甲、乙两人独立来该租车点租车骑游(各租一车一次).设甲、乙不超过两小时还车的概率分别为![]() ,
, ![]() ;两小时以上且不超过三小时还车的概率为
;两小时以上且不超过三小时还车的概率为![]() ,
, ![]() ;两人租车时间都不会超过四小时.
;两人租车时间都不会超过四小时.
(1)求甲、乙都在三到四小时内还车的概率和甲、乙两人所付租车费相同的概率;
(2)设甲、乙两人所付的租车费用之和为随机变量![]() ,求
,求![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() :
:  (
(![]() 为参数)和直线
为参数)和直线![]() :
: ![]() (
(![]() 为参数).
为参数).
(1)将曲线![]() 的方程化为普通方程;
的方程化为普通方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且
两点,且![]() 为弦
为弦![]() 的中点,求弦
的中点,求弦![]() 所在的直线方程.
所在的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网络营销部门为了统计某市网友2015年11月11日在某网店的网购情况,随机抽查了该市100名网友的网购金额情况,得到如下频率分布直方图.
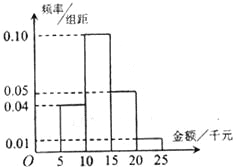
(1)估计直方图中网购金额的中位数;
(2)若规定网购金额超过15千元的顾客定义为“网购达人”,网购金额不超过15千元的顾客定义为“非网购达人”;若以该网店的频率估计全市“非网购达人”和“网购达人”的概率,从全市任意选取3人,则3人中“非网购达人”与“网购达人”的人数之差的绝对值为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)
某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率代替最高气温位于该区间的概率。
(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.学#科@网
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的偶函数f(x)满足f(x+1)= ![]() ,且f(x)在[﹣3,﹣2]上是减函数,若α,β是锐角三角形的两个内角,则( )
,且f(x)在[﹣3,﹣2]上是减函数,若α,β是锐角三角形的两个内角,则( )
A.f(sinα)>f(sinβ)
B.f(cosα)>f(cosβ)
C.f(sinα)>f(cosβ)
D.f(sinα)<f(cosβ)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=loga(ax+1)+mx是偶函数.
(1)求m;
(2)当a>1时,若函数f(x)的图像与直线l:y=﹣mx+n无公共点,求n的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的短轴长为
的短轴长为![]() ,右焦点为
,右焦点为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上异于左、右顶点
上异于左、右顶点![]() 的一点.
的一点.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与直线
与直线![]() 交于点
交于点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,证明:点
,证明:点![]() 关于直线
关于直线![]() 的对称点在直线
的对称点在直线![]() 上.
上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com