
 如图所示,在△ABC中,D、F分别是BC、AC的中点,
如图所示,在△ABC中,D、F分别是BC、AC的中点, =
=
 ,
, =
= ,
, =
= .
. 、
、 表示向量
表示向量 、
、 、
、 、
、 、
、 ;
;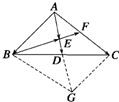 解:(1)如图所示:解延长AD到G,使
解:(1)如图所示:解延长AD到G,使 =
=
 ,
, =
= +
+ =
= ,
, =
=
 =
= (
( ),
), =
=
 =
= (
( ).
). =
=
 =
=
 ,
, =
= -
- =
= (
( )-
)- =
= (
(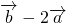 ).
). =
= -
- =
=
 -
- =
= (
(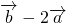 ).
). =
= (
(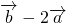 ),
), =
= (
(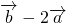 ).
). =
=
 ,即
,即 、
、 是共线向量,所以B、E、F三点共线.
是共线向量,所以B、E、F三点共线. ,由题意求出
,由题意求出 ,由F是AC的中点求出
,由F是AC的中点求出 ,再由向量减法的三角形法则求出
,再由向量减法的三角形法则求出 和
和 ;
; =
=
 ,故两个向量共线,即B、E、F三点共线.
,故两个向量共线,即B、E、F三点共线.

 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com