Question

5．已知点H（-1，0），点P在y轴上，动点M满足PH⊥PM，且直线PM与x轴交于点Q，Q是线段PM的中点．
（1）求动点M的轨迹E的方程；
（2）若点F是曲线E的焦点，过F的两条直线l₁，l₂关于x轴对称，且l₁交曲线E于A、C两点，l₂交曲线E于B、D两点，A、D在第一象限，若四边形ABCD的面积等于$\frac{5}{2}$，求直线l₁，l₂的方程．

Answer 1

分析 （1）由题意可知：$\overrightarrow{PH}$=（-1，-y₁），$\overrightarrow{PQ}$=（x₁，-y₁），利用PH⊥PM，求动点M的轨迹E的方程；
（2）由抛物线的焦点，设直线方程，代入椭圆方程，结合韦达定理，即可用m表示四边形ABCD的面积，求出m，即可求直线l₁，l₂的方程．

解答 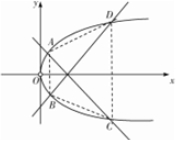解：（1）设M（x，y），P（0，y₁）（y₁≠0），Q（x₁，0），
$\overrightarrow{PH}$=（-1，-y₁），$\overrightarrow{PQ}$=（x₁，-y₁），
∵PH⊥PM，
∴-x₁+y′²=0，即y₁²=x₁，
又$\left\{\begin{array}{l}{\frac{x}{2}={x}_{1}}\\{\frac{y+{y}_{1}}{2}=0}\end{array}\right.$，则$\left\{\begin{array}{l}{{x}_{1}=\frac{x}{2}}\\{{y}_{1}=-y}\end{array}\right.$，可得：y²=$\frac{x}{2}$（x≠0），
（2）由（1）抛物线的焦点F（$\frac{1}{8}$，0），则直线l₁：x=my+$\frac{1}{8}$（m＞0），
则$\left\{\begin{array}{l}{x=my+\frac{1}{8}}\\{{y}^{2}=\frac{1}{2}x}\end{array}\right.$，整理得y²-$\frac{k}{2}$y-$\frac{1}{16}$=0，
∴y_A+y_C=$\frac{m}{2}$，y_Ay_C=-$\frac{1}{16}$，
由题意，四边形ABCD是等腰梯形，
∴S=丨$\frac{（2{y}_{A}+2{y}_{D}）（{x}_{D}-{x}_{A}）}{2}$丨=-2（y_A-y_C）²（y_A+y_C）=，
=-m[（y_A+y_C）²-4y_Ay_C]=-$\frac{{m}^{3}+m}{4}$，
由-$\frac{{m}^{3}+m}{4}$=$\frac{5}{2}$，
整理得：m³+m=10，（m+2）（m²-2m+5）=0，
则m²-2m+5＞0，则m=-2，
∴直线l₁，l₂的方程y=-$\frac{1}{2}$x+$\frac{1}{16}$，y=$\frac{1}{2}$x-$\frac{1}{16}$．

点评 本题考查轨迹方程，考查直线与抛物线的位置关系，考查韦达定理，考查面积的计算，属于中档题．