
分析 (Ⅰ)由已知条件,利用正弦定理,结合辅助角公式,即可求角B的值;
(Ⅱ)若a=2,且AC边上的中线BD长为$\sqrt{21}$,建立关于c的方程,利用三角形的面积公式求△ABC的面积.
解答 解:(Ⅰ)由已知条件得:$sinBcosC+\sqrt{3}sinBsinC-sinA-sinC=0$…(2分)
∴$sinBcosC+\sqrt{3}sinBsinC-sin(B+C)-sinC=0$…(3分)
即$\sqrt{3}sinBsinC-cosBsinC-sinC=0$.
∵sinC>0得$\sqrt{3}sinB-cosB=1$,∴$sin(B-\frac{π}{6})=\frac{1}{2}$…(5分)
又$B-\frac{π}{6}∈(0,\frac{5π}{6})$,∴$B-\frac{π}{6}=\frac{π}{6}$,∴$B=\frac{π}{3}$…(7分)
(II)由已知得:$\overrightarrow{BA}$+$\overrightarrow{BC}$=2$\overrightarrow{BD}$,平方得:$\overrightarrow{BA}$2+$\overrightarrow{BC}$2+2$\overrightarrow{BA}$•$\overrightarrow{BC}$=4$\overrightarrow{BD}$2,…(10分)
即c2+a2+2cacos$\frac{π}{3}$=84,
又a=2,∴c2+2c-80=0
解得:c=8或c=-2(舍去)…(12分)
∴S△ABC=$\frac{1}{2}acsinB$-$\frac{1}{2}×2×8×\frac{\sqrt{3}}{2}$=4$\sqrt{3}$.…(14分)
点评 本题考查正弦定理,辅助角公式,考查三角形的面积公式,考查学生分析解决问题的能力,属于中档题.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
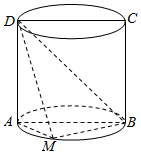 如图所示,已知四边形ABCD是圆柱的轴截面,M是下底面圆周上不与点A,B重合的点.
如图所示,已知四边形ABCD是圆柱的轴截面,M是下底面圆周上不与点A,B重合的点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com