
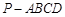 的底面是直角梯形,
的底面是直角梯形,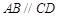 ,
,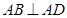 ,
,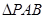 和
和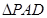 是两个边长为
是两个边长为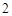 的正三角形,
的正三角形,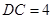 ,
,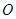 为
为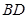 的中点,
的中点,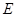 为
为 的中点.
的中点.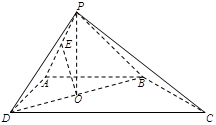
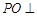 平面
平面 ;
;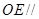 平面
平面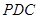 ;
;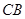 与平面
与平面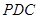 所成角的正弦值.
所成角的正弦值. 与平面
与平面 所成角的正弦值为
所成角的正弦值为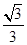 .
.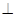 平面AEC,再根据线面垂直的性质定理证明AE
平面AEC,再根据线面垂直的性质定理证明AE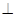 BC,根据勾股定理证明AE
BC,根据勾股定理证明AE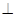 EC,利用线面垂直的判定定理证明AE
EC,利用线面垂直的判定定理证明AE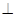 平面BCEF;(II)三棱锥体积利用体积转换为以E为顶点,
平面BCEF;(II)三棱锥体积利用体积转换为以E为顶点,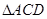 为底面的椎体体积求得.等体积转化,是立体几何经常运用的一种方法,高考也考过.
为底面的椎体体积求得.等体积转化,是立体几何经常运用的一种方法,高考也考过.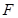 为
为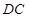 的中点,连接
的中点,连接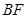 ,则
,则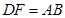 ,∵
,∵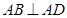 ,
,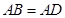 ,
,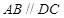 ,∴四边形
,∴四边形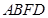 为正方形,∵
为正方形,∵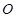 为
为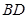 的中点,∴
的中点,∴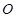 为
为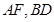 的交点,∵
的交点,∵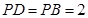 ,
, 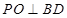 ,
,
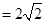 ,∴
,∴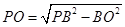
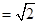 ,
,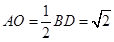 ,在三角形
,在三角形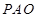 中,
中,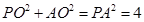 ,∴
,∴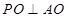 ,∵
,∵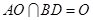 ,∴
,∴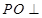 平面
平面 ;
; 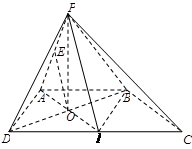
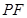 ,∵
,∵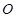 为
为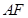 的中点,
的中点,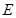 为
为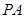 中点,∴
中点,∴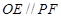 ,∵
,∵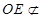 平面
平面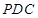 ,
,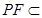 平面
平面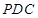 ,∴
,∴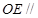 平面
平面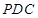 .方法2:由(Ⅰ)知
.方法2:由(Ⅰ)知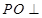 平面
平面 ,又
,又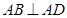 ,所以过
,所以过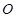 分别做
分别做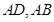 的平行线,以它们做
的平行线,以它们做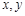 轴,以
轴,以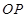 为
为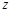 轴建立如图所示的空间直角坐标系,由已知得:
轴建立如图所示的空间直角坐标系,由已知得: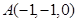 ,
,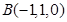 ,
,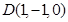
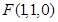 ,
,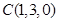 ,
,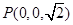 ,
,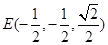 ,则
,则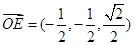 ,
,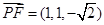 ,
,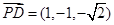 ,
,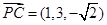 .∴
.∴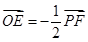 ∴
∴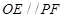 ∵
∵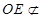 平面
平面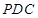 ,
,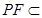 平面
平面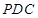 ,∴
,∴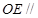 平面
平面 ;
; 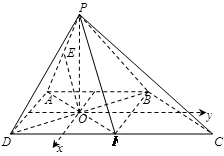
 的法向量为
的法向量为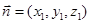 ,直线
,直线 与平面
与平面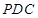 所成角
所成角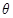 ,则
,则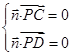 ,即
,即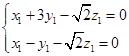 ,解得
,解得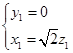 ,令
,令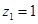 ,则平面
,则平面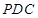 的一个法向量为
的一个法向量为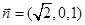 ,又
,又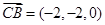
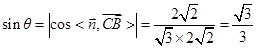 ,∴直线
,∴直线 与平面
与平面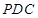 所成角的正弦值为
所成角的正弦值为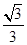 .
.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源:不详 题型:解答题
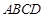 是菱形,
是菱形,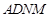 是矩形,平面
是矩形,平面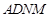 ⊥平面
⊥平面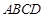 ,
,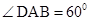 ,
,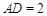 ,
,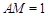 ,
,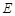 是
是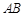 的中点.
的中点.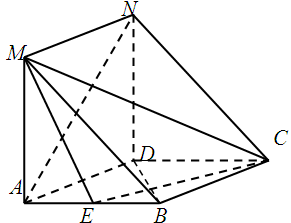
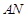 //平面
//平面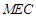 ;
;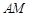 上是否存在点
上是否存在点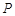 ,使二面角
,使二面角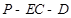 的大小为
的大小为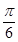 ?若存在,求出
?若存在,求出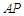 的长
的长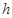 ;若不存在,请说明理由.
;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
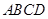 的4个顶点都在球
的4个顶点都在球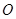 的表面上,
的表面上,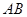 为球
为球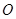 的直径,
的直径,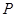 为球面上一点,且
为球面上一点,且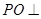 平面
平面 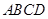 ,
,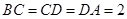 ,点
,点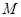 为
为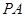 的中点.
的中点. 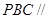 平面
平面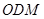 ;
;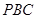 与平面
与平面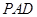 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
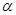 外有两条直线
外有两条直线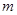 和
和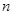 ,如果
,如果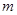 和
和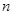 在平面
在平面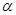 内的射影分别是
内的射影分别是 和
和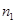 ,给出下列四个命题:①
,给出下列四个命题:① ②
② ③
③ 与
与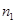 相交
相交
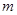 与
与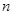 相交或重合 ④
相交或重合 ④ 与
与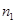 平行
平行
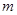 与
与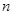 平行或重合,其中不正确的命题的个数是( )
平行或重合,其中不正确的命题的个数是( )| A.4个 | B.3个 | C.2个 | D. 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com