
分析 Sn=2an-2,n=1时,a1=2a1-2,解得a1.n≥2时,an=Sn-Sn-1,再利用等比数列的通项公式可得an.令bn≥0,解得n,即可得出.
解答 解:∵Sn=2an-2,∴n=1时,a1=2a1-2,解得a1=2.
n≥2时,an=Sn-Sn-1=2an-2-(2an-1-2),∴an=2an-1.
∴数列{an}是等比数列,公比为2.
∴an=2n.
∴bn=10-log2an=10-n.
由bn=10-n≥0,解得n≤10.
∴使数列{bn}的前n项和取最大值时的n的值为9或10.
故答案为:9或10.
点评 本题考查了数列递推关系、等比数列的通项公式、不等式的解法、数列的单调性,考查了推理能力与计算能力,属于中档题.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:选择题
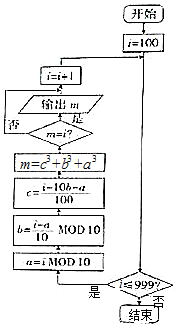 运行如图所示的程序框图,输出的数称为“水仙花数”.(算术符号MOD表示取余数,如11MOD2=1).下列数中的“水仙花数”是( )
运行如图所示的程序框图,输出的数称为“水仙花数”.(算术符号MOD表示取余数,如11MOD2=1).下列数中的“水仙花数”是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知三棱柱ABC-A1B1C1中,AB=AC=AA1=2,侧面ABB1A1⊥底面ABC,D是BC的中点,∠BAA1=120o,B1D⊥AB.
已知三棱柱ABC-A1B1C1中,AB=AC=AA1=2,侧面ABB1A1⊥底面ABC,D是BC的中点,∠BAA1=120o,B1D⊥AB.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,1,2} | B. | {-1,2} | C. | {1,2} | D. | {-1,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com