
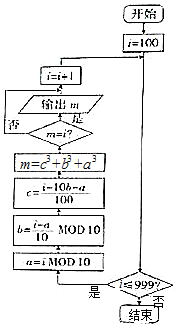
 运行如图所示的程序框图,输出的数称为“水仙花数”.(算术符号MOD表示取余数,如11MOD2=1).下列数中的“水仙花数”是( )
运行如图所示的程序框图,输出的数称为“水仙花数”.(算术符号MOD表示取余数,如11MOD2=1).下列数中的“水仙花数”是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 152 | B. | 135 | C. | 80 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
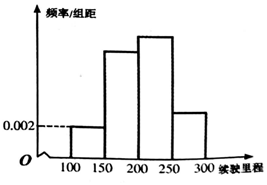 持续性的雾霾天气严重威胁着人们的身体健康,汽车排放的尾气是造成雾霾天气的重要因素之一.为了贯彻落实国务院关于培育战略性新兴产业和加强节能减排工作的部署和要求,中央财政安排专项资金支持开展私人购买新能源汽车补贴试点.2017年国家又出台了调整新能源汽车推广应用财政补贴的新政策,其中新能源乘用车推广应用补贴标准如表:
持续性的雾霾天气严重威胁着人们的身体健康,汽车排放的尾气是造成雾霾天气的重要因素之一.为了贯彻落实国务院关于培育战略性新兴产业和加强节能减排工作的部署和要求,中央财政安排专项资金支持开展私人购买新能源汽车补贴试点.2017年国家又出台了调整新能源汽车推广应用财政补贴的新政策,其中新能源乘用车推广应用补贴标准如表:| 纯电动续驶里程R(公里) | 100≤R<150 | 150≤R<250 | R>250 |
| 补贴标准(万元/辆) | 2 | 3.6 | 44 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com