
 �����Ե���������������в�����ǵ����彡���������ŷŵ�β�������������������Ҫ����֮һ��Ϊ�˹᳹��ʵ����Ժ��������ս�������˲�ҵ�ͼ�ǿ���ܼ��Ź����IJ����Ҫ�������������ר���ʽ�֧�ֿ�չ˽�˹�������Դ���������Ե㣮2017������ֳ�̨�˵�������Դ�����ƹ�Ӧ�ò��������������ߣ���������Դ���ó��ƹ�Ӧ�ò����������
�����Ե���������������в�����ǵ����彡���������ŷŵ�β�������������������Ҫ����֮һ��Ϊ�˹᳹��ʵ����Ժ��������ս�������˲�ҵ�ͼ�ǿ���ܼ��Ź����IJ����Ҫ�������������ר���ʽ�֧�ֿ�չ˽�˹�������Դ���������Ե㣮2017������ֳ�̨�˵�������Դ�����ƹ�Ӧ�ò��������������ߣ���������Դ���ó��ƹ�Ӧ�ò����������| ���綯��ʻ���R����� | 100��R��150 | 150��R��250 | R��250 |
| ����������Ԫ/���� | 2 | 3.6 | 44 |
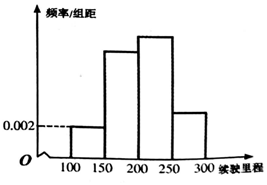
���� ��1���ɱ���ֱ������һ�顢�ڶ��顢�����顢�������Ƶ�ʣ��ɴ�����Ƶ�ʷֲ�ֱ��ͼ�ܹ�����20�����綯���ó���ƽ����ʻ��̣�
��2��������֪�εĿ���ȡֵΪ2��3.6��4.4���ֱ������Ӧ�ĸ��ʣ��ɴ�������εķֲ��к���ѧ������
��� �⣺��1���ɱ���֪��һ���Ƶ��Ϊ0.1���ڶ����Ƶ��Ϊ$\frac{7}{20}=0.35$��
�������Ƶ��Ϊ0.4���������Ƶ��Ϊ0.15��
��Ƶ�ʷֲ�ֱ��ͼ������20�����綯���ó���ƽ����ʻ���Ϊ��
125��0.1+175��0.35+225��0.4+275��0.15=205�������
��2��������֪�εĿ���ȡֵΪ2��3.6��4.4��
P����=2��=0.1��
P����=3.6��=0.75��
P����=4.4��=0.15��
��εķֲ���Ϊ��
| �� | 2 | 3.6 | 4.4 |
| P | 0.1 | 0.75 | 0.15 |
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ��Ӧ�ã�������ɢ����������ķֲ��м���ѧ�����������е��⣬����ʱҪ�������⣬ע��Ƶ�ʷֲ�ֱ��ͼ�����ʵĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-1��1�� | B�� | ��-1��1] | C�� | [1��2�� | D�� | [1��2] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
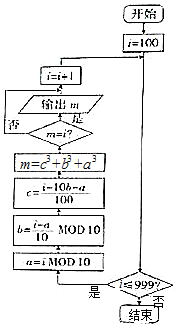 ������ͼ��ʾ�ij����ͼ�����������Ϊ��ˮ�ɻ�����������������MOD��ʾȡ��������11MOD2=1�����������еġ�ˮ�ɻ������ǣ�������
������ͼ��ʾ�ij����ͼ�����������Ϊ��ˮ�ɻ�����������������MOD��ʾȡ��������11MOD2=1�����������еġ�ˮ�ɻ������ǣ�������| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 36�� | B�� | 16�� | C�� | $\frac{9��}{2}$ | D�� | $\frac{9��}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 21 | B�� | 35 | C�� | 63 | D�� | 126 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com