
分析 (1)由椭圆的离心率$e=\frac{{\sqrt{2}}}{2}$,得b=c,写出以上顶点和右焦点为直径端点的圆的方程,再由点到直线的距离列式求得b,c的值,结合隐含条件求得a,则椭圆方程可求;
(2)由题意设A(x1,y1),B(x2,y2),直线AB方程为:y=-x+n.联立$\left\{\begin{array}{l}y=-x+n\\ \frac{x^2}{2}+{y^2}=1\end{array}\right.$消y整理可得:3x2-4nx+2n2-2=0,由△>0解得n的范围.再由根与系数的关系结合中点坐标公式求得直线AB之中点坐标,代入直线AB,再由点P在直线l上求得m的范围,最后由3$\overrightarrow{QA}$•$\overrightarrow{QB}$=32求得m的值.
解答 解:(1)由椭圆的离心率$e=\frac{{\sqrt{2}}}{2}$,得$\frac{c^2}{a^2}=\frac{c^2}{{{b^2}+{c^2}}}=\frac{1}{2}$,得b=c.
上顶点为(0,b),右焦点为(b,0),
以上顶点和右焦点为直径端点的圆的方程为${({x-\frac{b}{2}})^2}+{({y-\frac{b}{2}})^2}={({\frac{a}{2}})^2}=\frac{b^2}{2}$,
∴$\frac{{|{b-2}|}}{{\sqrt{2}}}=\frac{{\sqrt{2}}}{2}b$,即|b-2|=b,得b=c=1,$a=\sqrt{2}$,
∴椭圆的标准方程为$\frac{x^2}{2}+{y^2}=1$;
(2)由题意设A(x1,y1),B(x2,y2),直线AB方程为:y=-x+n.
联立$\left\{\begin{array}{l}y=-x+n\\ \frac{x^2}{2}+{y^2}=1\end{array}\right.$消y整理可得:3x2-4nx+2n2-2=0,
由△=(-4n)2-12(2n2-2)=24-8n2>0,解得$-\sqrt{3}<n<\sqrt{3}$.
${x_1}+{x_2}=\frac{4n}{3}$,${x_1}{x_2}=\frac{{2{n^2}-2}}{3}$,
设直线AB之中点为P(x0,y0),则${x_0}=\frac{{{x_1}+{x_2}}}{2}=\frac{2n}{3}$,
由点P在直线AB上得:${y_0}=-\frac{2n}{3}+n=\frac{n}{3}$,
又点P在直线l上,∴$\frac{n}{3}=\frac{2n}{3}+m$,则$m=-\frac{n}{3}∈({-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}})$…①.
又$\overrightarrow{QA}=({{x_1},{y_1}-3})$,$\overrightarrow{QB}=({{x_2},{y_2}-3})$,
∴$\overrightarrow{QA}•\overrightarrow{QB}-\frac{32}{3}=({{x_1},{y_1}-3})•({{x_2},{y_2}-3})-\frac{32}{3}$
=${x_1}{x_2}+({{y_1}-3})({{y_2}-3})-\frac{32}{2}={n^2}-2n-3=9{m^2}+6m-3=3({3m-1})({m+1})=0$,
解得:$m=\frac{1}{3}$或m=-1…②
综合①②,知m的值为$\frac{1}{3}$.
点评 本题考查椭圆的简单性质,考查直线与椭圆位置关系的应用,训练了平面向量在求解圆锥曲线问题中的应用,是中档题.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:选择题
| x | 18 | 13 | 10 | -1 |
| y | 24 | 34 | 38 | 64 |
| A. | 65度 | B. | 68度 | C. | 70度 | D. | 72度 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
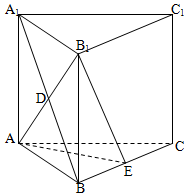 在直三棱柱ABC-A1B1C1中,AA1=AB=AC=4,∠BAC=90°,D为侧面ABB1A1的中心,E为BC的中点
在直三棱柱ABC-A1B1C1中,AA1=AB=AC=4,∠BAC=90°,D为侧面ABB1A1的中心,E为BC的中点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{12}$ | B. | $\frac{12}{13}$ | C. | $-\frac{5}{13}$ | D. | $-\frac{12}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
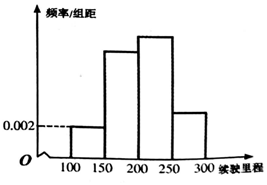 持续性的雾霾天气严重威胁着人们的身体健康,汽车排放的尾气是造成雾霾天气的重要因素之一.为了贯彻落实国务院关于培育战略性新兴产业和加强节能减排工作的部署和要求,中央财政安排专项资金支持开展私人购买新能源汽车补贴试点.2017年国家又出台了调整新能源汽车推广应用财政补贴的新政策,其中新能源乘用车推广应用补贴标准如表:
持续性的雾霾天气严重威胁着人们的身体健康,汽车排放的尾气是造成雾霾天气的重要因素之一.为了贯彻落实国务院关于培育战略性新兴产业和加强节能减排工作的部署和要求,中央财政安排专项资金支持开展私人购买新能源汽车补贴试点.2017年国家又出台了调整新能源汽车推广应用财政补贴的新政策,其中新能源乘用车推广应用补贴标准如表:| 纯电动续驶里程R(公里) | 100≤R<150 | 150≤R<250 | R>250 |
| 补贴标准(万元/辆) | 2 | 3.6 | 44 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com