
分析 (Ⅰ)依题意原点O到切线l:y=-$\frac{1}{2}$x+m的距离为半径1,⇒m=$\frac{\sqrt{5}}{2}$,⇒A(0,$\frac{\sqrt{5}}{2}$),B($\sqrt{5}$,0)
代入椭圆方程,求出a、b即可
(2)由原点O到切线l:y=kx+m的距离为半径r⇒m2=(1+k2)r2.联立直线方程和与椭圆的方程,利用$\overrightarrow{OA}•\overrightarrow{OB}=0$求解.
解答 解:(Ⅰ)依题意原点O到切线l:y=-$\frac{1}{2}$x+m的距离为半径1,∴$\frac{m}{\sqrt{1+\frac{1}{4}}}=1$,⇒m=$\frac{\sqrt{5}}{2}$,
切线l:y=-$\frac{1}{2}$x+$\frac{\sqrt{5}}{2}$,⇒A(0,$\frac{\sqrt{5}}{2}$),B($\sqrt{5}$,0)
∴a=$\sqrt{5}$,b=$\frac{\sqrt{5}}{2}$,∴椭圆E的方程为:$\frac{{x}^{2}}{5}+\frac{{y}^{2}}{\frac{5}{4}}=1$.
(Ⅱ)设A(x1,y1),B(x2,y2),
联立$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$,得(b2+a2k2)x2+2a2kmx+a2m2-a2b2=0.
$△=(2{a}^{2}km)^{2}-4({b}^{2}+{a}^{2}{k}^{2})({a}^{2}{m}^{2}-{a}^{2}{b}^{2})\\;>0$.
${x}_{1}+{x}_{2}=\frac{-2{a}^{2}km}{{b}^{2}+{a}^{2}{k}^{2}},{x}_{1}{x}_{2}=\frac{{a}^{2}{m}^{2}-{a}^{2}{b}^{2}}{{b}^{2}+{a}^{2}{k}^{2}}$.
∵以AB为直径的圆经过坐标原点O,∴$\overrightarrow{OA}•\overrightarrow{OB}={x}_{1}{x}_{2}+{y}_{1}{y}_{2}=0$;
⇒(k2+1)x1x2+km(x1+x2)=m2(a2+b2)=(k2+1)a2b2…①
又∵圆O的一条切线l:y=kx+m,∴原点O到切线l:y=kx+m的距离为半径r⇒m2=(1+k2)r2…②
由①②得r2(a2+b2)=a2b2.
∴以AB为直径的圆经过坐标原点O,则a,b,r之间的等量关为:r2(a2+b2)=a2b2.
点评 本题考查曲线方程的求法,考查了直线与圆锥曲线位置关系的应用,训练了平面向量在求解圆锥曲线问题中的应用,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | {-2}∪[2,+∞) | B. | (-∞,-2)∪[2,+∞) | C. | [2,+∞) | D. | {0}∪[2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
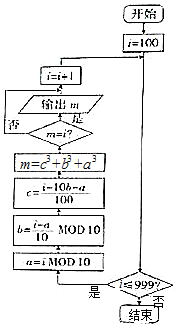 运行如图所示的程序框图,输出的数称为“水仙花数”.(算术符号MOD表示取余数,如11MOD2=1).下列数中的“水仙花数”是( )
运行如图所示的程序框图,输出的数称为“水仙花数”.(算术符号MOD表示取余数,如11MOD2=1).下列数中的“水仙花数”是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com