练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．已知等比数列{an}的前n项和为Sn，a1+a3=30，S4=120，设bn=1+log3an，那么数列{bn}的前15项和为（　　）
    A．152B．135C．80D．16

    分析 设等比数列{an}的公比为q，则q≠1．由a1+a3=30，S4=120，可得${a}_{1}（1+{q}^{2}）$=30，${a}_{1}（1+q+{q}^{2}+{q}^{3}）$=120，解得a1，q．进而得出．

    解答 解：设等比数列{an}的公比为q，则q≠1．
    ∵a1+a3=30，S4=120，∴${a}_{1}（1+{q}^{2}）$=30，${a}_{1}（1+q+{q}^{2}+{q}^{3}）$=120，
    解得a1=q=3．
    ∴an=3n．
    设bn=1+log3an=1+n
    那么数列{bn}的前15项和=$\frac{15×（2+16）}{2}$=135．
    故选：B．

    点评 本题考查了等比数列的通项公式、等差数列的求和公式、对数的运算性质，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    1．一已知等差数列{an}中，其前n项和为Sn，若a3+a4+a5=42，则S7=（　　）
    A．98B．49C．14D．147

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．在△ABC中，已知AB=8，AC=6，点O为三角形的外心，则$\overrightarrow{BC}•\overrightarrow{OA}$=14．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．在实数集R中，已知集合$A=\{x|x\sqrt{{x^2}-4}≥0\}$和集合B={x||x-1|+|x+1|≥2}，则A∩B=（　　）
    A．{-2}∪[2，+∞）B．（-∞，-2）∪[2，+∞）C．[2，+∞）D．{0}∪[2，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．把A，B，C，D 4张纸牌随机地分发给甲，乙，丙，丁四个人，每人一张，则事件“乙分得A牌”与事件“丁分得A牌”是（　　）
    A．不可能事件B．互斥但不对立事件
    C．对立事件D．以上答案都不对

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知全集为R，且集合A={x|log2（x+1）＜2}，$B=\{x|\frac{x-2}{x-1}≥0\}$，则A∩（∁RB）等于（　　）
    A．（-1，1）B．（-1，1]C．[1，2）D．[1，2]

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．函数f（x）（x∈R）满足f（1）=2且f（x）在R上的导数f'（x）满足f'（x）-3＞0，则不等式f（log3x）＜3log3x-1的解集为（0，3）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．“|x+1|+|x-2|≤5”是“-2≤x≤3”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

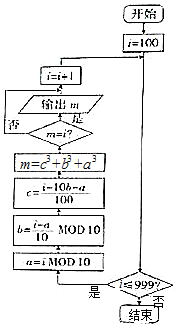    19．运行如图所示的程序框图，输出的数称为“水仙花数”．（算术符号MOD表示取余数，如11MOD2=1）．下列数中的“水仙花数”是（　　）
    ①“水仙花数”是三位数；
    ②152是“水仙花数”；
    ③407是“水仙花数”．
    A．0B．1C．2D．3

    查看答案和解析>>

    同步练习册答案