
【题目】设函数![]() ,
,![]() .
.
(1)讨论![]() 在
在![]() 上的单调性;
上的单调性;
(2)当![]() 时,若存在正实数
时,若存在正实数![]() ,使得对
,使得对![]() ,都有
,都有![]() ,求
,求![]() 的取值范围..
的取值范围..
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)求得![]() ,然后分
,然后分![]() 和
和![]() 两种情况讨论,分析导数在区间
两种情况讨论,分析导数在区间![]() 上的符号变化,即可得出函数
上的符号变化,即可得出函数![]() 在区间
在区间![]() 上的单调区间;
上的单调区间;
(2)由(1)可知,当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,则
上单调递减,则![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ,构造函数
,构造函数![]() ,分
,分![]() 和
和![]() 两种情况讨论,分析函数
两种情况讨论,分析函数![]() 的单调性,结合
的单调性,结合![]() 在区间
在区间![]() 上恒成立可求得实数
上恒成立可求得实数![]() 的取值范围.
的取值范围.
(1)由![]() ,得
,得![]() ,
,![]() ,
,![]() ,
,
当![]() 时,由
时,由![]() ,得
,得![]() ,即函数
,即函数![]() 在
在![]() 上单调递增,
上单调递增,
由![]() ,得
,得![]() ,即函数
,即函数![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() 在
在![]() 上恒成立,即函数
上恒成立,即函数![]() 在
在![]() 上单调递增.
上单调递增.
综上所述,当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
(2)![]() ,当
,当![]() 时,由(1)结合函数
时,由(1)结合函数![]() 的单调性知,
的单调性知,
![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ,则由
,则由![]() 得
得![]() .
.
设![]() ,则
,则![]() ,
,
由![]() 得
得![]() ,由
,由![]() 得
得![]() .
.
(Ⅰ)若![]() ,则
,则![]() ,故
,故![]() ,即函数
,即函数![]() 在
在![]() 上单调递减,
上单调递减,
![]() ,
,![]() 对任意
对任意![]() ,都有
,都有![]() ,不合题意;
,不合题意;
(Ⅱ)若![]() ,则
,则![]() ,故
,故![]() ,
,
![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,
,![]() 对任意
对任意![]() ,都有
,都有![]() ,符合题意,
,符合题意,
此时取![]() ,可使得对
,可使得对![]() ,都有
,都有![]() .
.
综上可得![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥中,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点.
的中点.
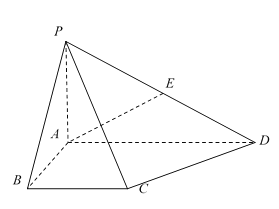
(Ⅰ)求直线![]() 与平面
与平面![]() 所成角的余弦值;
所成角的余弦值;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)若![]() 在段
在段![]() 上,且直线
上,且直线![]() 与平面
与平面![]() 相交,求
相交,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设实数列![]() 满足
满足![]() ,则下面说法正确的是( )
,则下面说法正确的是( )
A.若![]() ,则
,则![]() 前2019项中至少有1010个值相等
前2019项中至少有1010个值相等
B.若![]() ,则当
,则当![]() 确定时,一定存在实数
确定时,一定存在实数![]() 使
使![]() 恒成立
恒成立
C.若![]() ,
,![]() 一定为等比数列
一定为等比数列
D.若![]() ,则当
,则当![]() 确定时,一定存在实数
确定时,一定存在实数![]() 使
使![]() 恒成立
恒成立
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据全球摩天大楼的统计,至2019年,安徽省合肥市的摩天大楼已经有95座在中国城市中排名第10位,全球排名第15位,目前合肥恒大中心建设中的最高楼,外形设计成了“竹节”的形态,既体现了力量超凡,又象征着向上生长的强烈意志,更预示了未来的繁荣和兴旺.它与传承千年的“微文化”相得益建成后将跻身世界十大摩天大楼之列,若大楼由9节“竹节”组成,最上部分的4节高228米,最下部分3节高204米,且每一节高度变化均匀(即每节高度自上而下成等差数列),则该摩天大楼的总高度为( )
A.518米B.558米C.588米D.668米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com