
【题目】在三棱锥![]() 中,
中,![]() ,侧棱
,侧棱![]() 与底面
与底面![]() 所成的角为
所成的角为![]() ,则该三棱锥外接球的体积为__________.
,则该三棱锥外接球的体积为__________.
【答案】![]()
【解析】
过点P作PH⊥平面ABC于H,可得∠PAH是直线PA与底面ABC所成的角,得![]() .由PA=PB=PC,得外接球心O必定在PH上,连接OA,可得△POA是底角等于30°的等腰三角形,从而得到外接球的半径R=OA=1,再用球的体积公式可得该三棱锥外接球的体积.
.由PA=PB=PC,得外接球心O必定在PH上,连接OA,可得△POA是底角等于30°的等腰三角形,从而得到外接球的半径R=OA=1,再用球的体积公式可得该三棱锥外接球的体积.
过点P作PH⊥平面ABC于H,
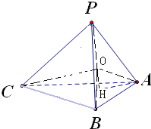
∵AH是PA在平面ABC内的射影,
![]() 是直线PA与底面ABC所成的角,得
是直线PA与底面ABC所成的角,得![]() ,
,
![]() 中,
中,![]() ,
,![]() ,
,
设三棱锥外接球的球心为O,
∵PA=PB=PC,
∴P在平面ABC内的射影H是![]() 的外心
的外心
由此可得,外接球心O必定在PH上,连接OA、OB、OC,
![]() 中,OP=OA,
中,OP=OA,
∴∠OAP=∠OPA=30°,可得![]()
∴三棱锥外接球的半径R=OA=1
因此该三棱锥外接球的体积为![]() .
.
故答案为:![]() .
.


科目:高中数学 来源: 题型:
【题目】如图是2017年第一季度五省GDP情况图,则下列陈述中不正确的是( )
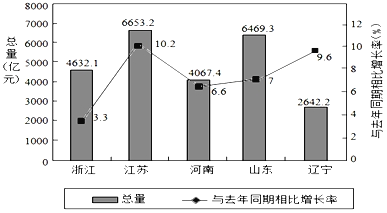
A.2017年第一季度GDP增速由高到低排位第5的是浙江省.
B.与去年同期相比,2017年第一季度的GDP总量实现了增长.
C.2017年第一季度GDP总量和增速由高到低排位均居同一位的省只有1个
D.去年同期河南省的GDP总量不超过4000亿元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明口袋中有3张10元,3张20元(因纸币有编号认定每张纸币不同),现从中掏出纸币超过45元的方法有_______种;若小明每次掏出纸币的概率是等可能的,不放回地掏出4张,刚好是50元的概率为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 是定义在
是定义在![]() 上的单调函数,且对于任意正数
上的单调函数,且对于任意正数![]() 有
有![]() ,已知
,已知![]() ,若一个各项均为正数的数列
,若一个各项均为正数的数列![]() 满足
满足![]() ,其中
,其中![]() 是数列
是数列![]() 的前
的前![]() 项和,则数列
项和,则数列![]() 中第18项
中第18项![]() ( )
( )
A. ![]() B. 9 C. 18 D. 36
B. 9 C. 18 D. 36
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为比较甲、乙两地某月14时的气温状况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图.考虑以下结论:
①甲地该月14时的平均气温低于乙地该月14时的平均气温;
②甲地该月14时的平均气温高于乙地该月14时的平均气温;
③甲地该月14时的平均气温的标准差小于乙地该月14时的气温的标准差;
④甲地该月14时的平均气温的标准差大于乙地该月14时的气温的标准差.
其中根据茎叶图能得到的统计结论的标号为( )
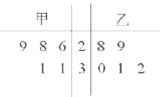
A.①③B.①④C.②③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一段南北两岸互相平行、宽度为![]() 的景观河.靠南岸水域有一半径为
的景观河.靠南岸水域有一半径为![]() 半圆形亲水平台,圆心
半圆形亲水平台,圆心![]() 在南岸边上,北岸边有一风雨亭
在南岸边上,北岸边有一风雨亭![]() (底座大小忽略不计),风雨亭
(底座大小忽略不计),风雨亭![]() 距位于北岸边上的
距位于北岸边上的![]() 点
点![]() (
(![]() 在
在![]() 的正北方,
的正北方,![]() 在
在![]() 的右侧).为了方便市民休闲,现决定修建折线型步行栈道
的右侧).为了方便市民休闲,现决定修建折线型步行栈道![]() (图中粗线所示),其中
(图中粗线所示),其中![]() 与圆
与圆![]() 相切,
相切,![]() 段的造价为4万元/
段的造价为4万元/![]() ,
,![]() 段和
段和![]() 段分别在南北两岸边上(其中
段分别在南北两岸边上(其中![]() 为半圆
为半圆![]() 的一条直径的左端点),
的一条直径的左端点),![]() 段和
段和![]() 段的造价都为2万元/
段的造价都为2万元/![]() .记
.记![]() 为
为![]() ,
,![]() .
.
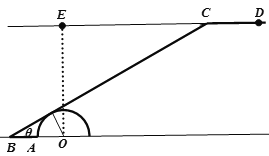
(1)若![]() ,求栈道
,求栈道![]() 段的长;
段的长;
(2)设三段栈道总造价为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,
中,![]() 是过定点
是过定点![]() 且倾斜角为
且倾斜角为![]() 的直线;在极坐标系(以坐标原点
的直线;在极坐标系(以坐标原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴,取相同单位长度)中,曲线
轴非负半轴为极轴,取相同单位长度)中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的参数方程,并将曲线
的参数方程,并将曲线![]() 的方程化为直角坐标方程;
的方程化为直角坐标方程;
(2)若曲线![]() 与直线
与直线![]() 相交于不同的两点
相交于不同的两点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com